6. Wellbore Stability

6.1 The wellbore environment

Wellbore stability is critical for drilling. A stable open-hole requires the surrounding sediment and rock to bear the stresses that amplify around the wellbore cavity. The surrounding rock must hold stresses until casing is set or for undetermined time if left uncased.

Wellbore stability depends on two set of variables (Figure 6.1): one set which is out of our control and another set of variables that we can control.

• In-situ variables out of our control include far-field stresses $\uuline{S}{}_G$, pore presssure $P_p$, and rock properties.
• Controllable variables include mud pressure $P_W$ ($W$ for wellbore), mud composition, mud fluid chemistry, and wellbore orientation (direction azimuth and deviation).

Figure 6.1: Wellbore stability analysis includes inherent variables, such as in-situ stresses and rock properties, and controllable variables, such as wellbore orientation and mud pressure during drilling.

The pressure in the wellbore $P_W$ is one of the main variables to maintain wellbore stability. Mud (mass) density and vertical depth $z$ (TVD) determine the mud hydrostatic pressure (in the absence of additional pressure controls at the surface - such as in managed pressure drilling):

$$P_W = \rho_{mud} \: g \: z$$ (6.1)

The pressure gradient within the wellbore is proportional to mud density $dP_W/dz = \rho_{mud} g$ (Fig. 6.2). This quantity is usually measured and reported in p.p.g. (pounds-force per gallon). For example the pressure gradient for fresh water is 9,800 N/m$^3$ (= 9.8 MPa/km = 0.44 psi/ft), about 8.3 ppg. The lithostatic gradient of 1 psi/ft is equivalent to 1 (psi/ft) $\times$ (8.3 ppg/0.44 (psi/ft)) = 18.9 ppg. The “equivalent circulation density” is also reported in ppg and take into account pressure drops in the annulus.

Figure 6.2: Wellbore mud pressure and equivalent density. Mud pressure $P_W$ is usually reported in terms of gradient (depth-independent) rather than in absolute values.

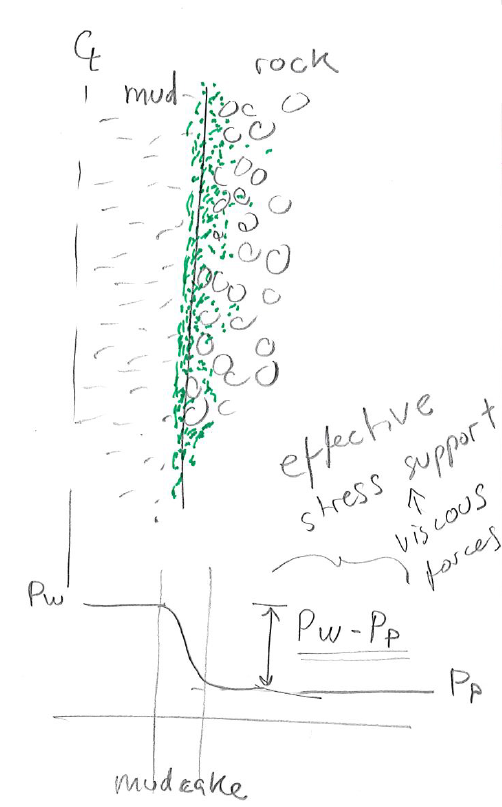
Over-balanced drilling implies $P_W > P_p$. Over-balanced drilling favors the formation of a “mud-cake” or “filter-cake” on the wall of the wellbore which permits adding stress support on the wellbore wall approximately equal to $P_W - P_p$ (Fig. 6.4). The resulting effect is similar to an impermeable and elastic membrane applying a stress on the wellbore wall (similar to the membranes used in triaxial tests). Under-balanced drilling $P_W < P_p$ may be preferred in some specific instances.

Figure 6.3: Leak-off of mud filtrate favors clogging of mud particulates which help apply a normal stress on the wellbore wall. This layer of particulates is called mud-cake.

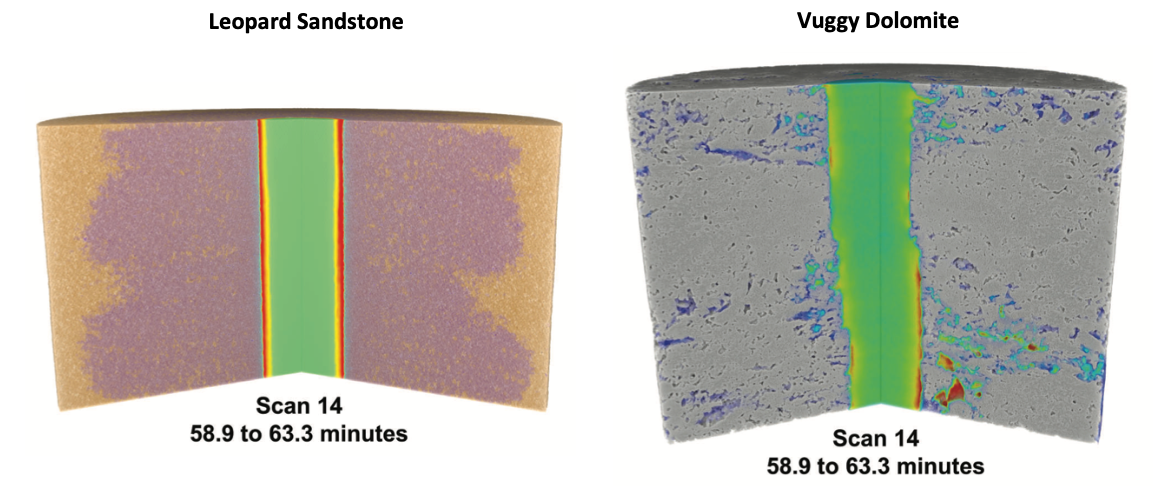
Figure 6.4: Examples of mud buildup (warm colors) and filtrate/leak-off (cool colors) in two different rock samples as imaged trough time-lapse X-ray tomography. The buildup of mud with time makes the mudcake or filtercake. Image credit: https://doi.org/10.30632/PJV63N5-2022a4.

6.2 Kirsch solution for stresses around a cylindrical cavity

6.2.1 Cylindrical coordinate system

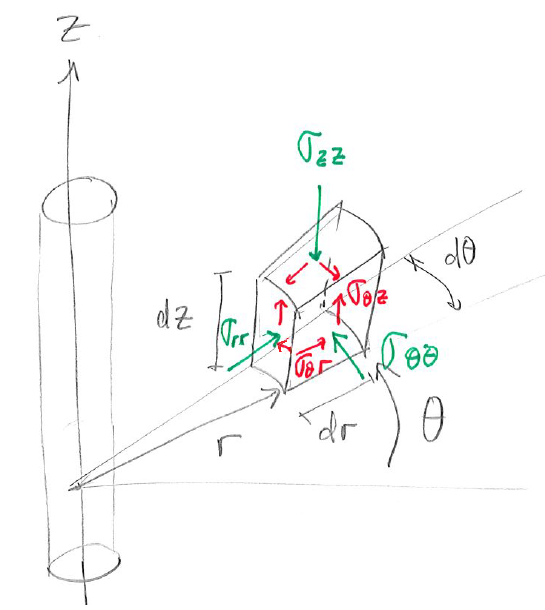
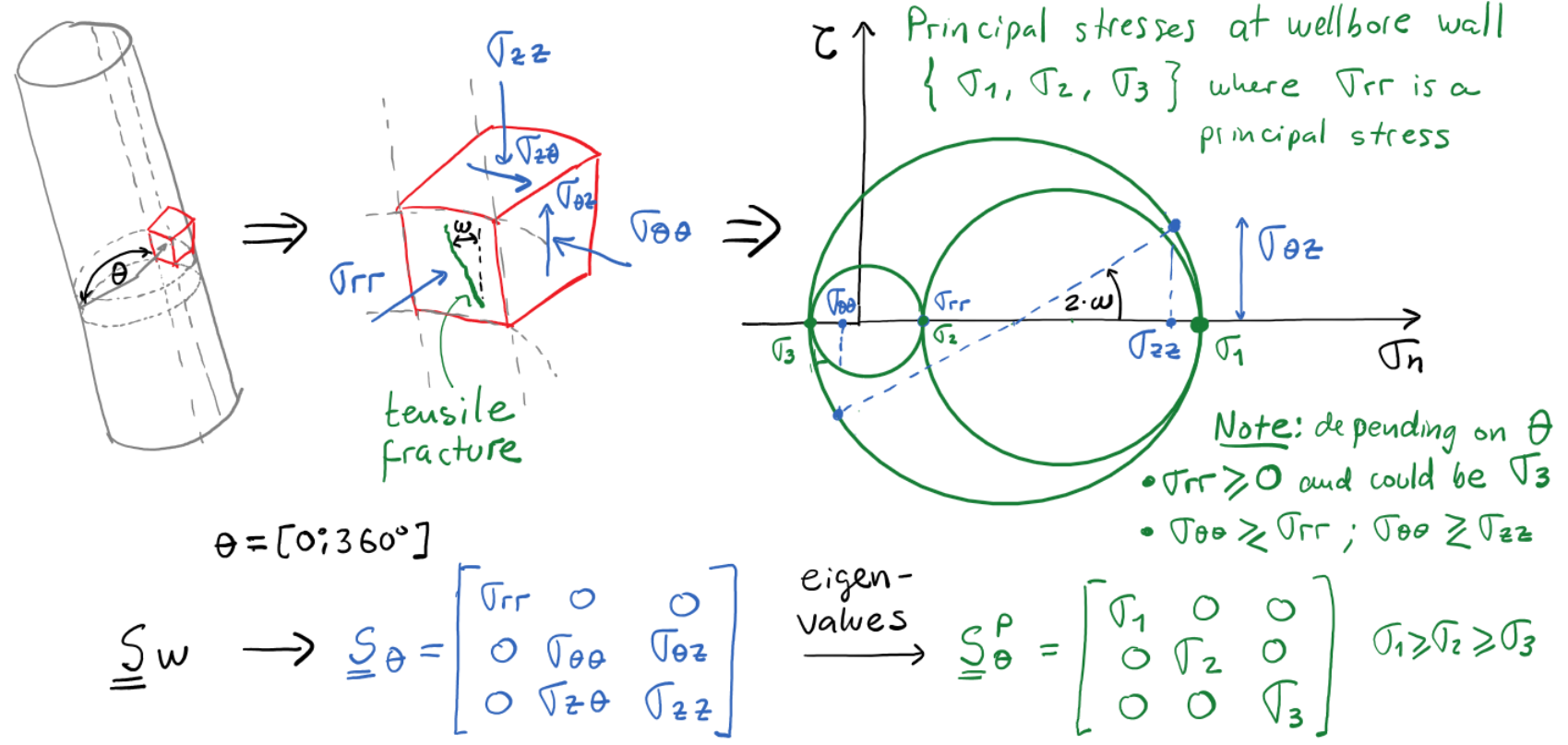
The cylindrical symmetry of a wellbore prompts the utilization of a cylindrical coordinate system rather than a rectangular cartesian coordinate system. The volume element of stresses in cylindrical coordinates is shown in Fig. 6.5. The distance $r$ is measured from the center axis of the wellbore. The angle $\theta$ is measured with respect to a predefined plane.

Figure 6.5: Infinitesimal volume element in cylindrical coordinates and associated normal and shear stresses.

The normal stresses are radial stress $\sigma _{rr}$, tangential or hoop stress $\sigma _{\theta \theta }$, and axial stress $\sigma_{zz}$. The shear stresses are $\sigma _{r\theta }$, $\sigma_{r z}$, and $\sigma_{\theta z}$.

6.2.2 Kirsch solution components

The Kirsch solution allows us to calculate normal and shear stresses around a circular cavity in a homogeneous linear elastic solid . The complete Kirsch solution assumes independent action of multiple factors, namely far-field isotropic stress, deviatoric stress, wellbore pressure and pore pressure.

1. Isotropic far-field stress: The solution for a compressive isotropic far field stress $\sigma _{\infty }$ is shown in Fig. 6.6. The presence of the wellbore amplifies compressive stresses 2 times $\sigma_{\theta \theta}/\sigma_{\infty}=2$ all around the wellbore wall in circumferential direction. The presence of the wellbore cavity also creates infinitely large stress anisotropy at the wellbore wall $\sigma_{\theta \theta}/\sigma_{rr}= \infty$ all around the wellbore wall, since $\sigma_{rr}=0$ in this case. Stresses decrease inversely proportional to $r^2$ and are neglible at $\sim$4 radii from the wellbore wall.

   Figure 6.6: Kirsch solution for far field isotropic stress $\sigma _{\infty }$.

   

2. Inner wellbore pressure: The solution for fluid wall pressure in the wellbore $P_W$ is shown in Fig. 6.7. We assume a non-porous solid now. This assumption will be relaxed later on. Wellbore pressure adds compression on the wellbore wall $\sigma_{rr} = +P_W$, and induces cavity expansion and tensile hoop stresses $\sigma_{\theta\theta} = - P_W$ all around the wellbore.

   Figure 6.7: Kirsch solution for wellbore pressure $P_W$.

   

3. Deviatoric stress: The solution for a deviatoric stress $\Delta \sigma$ aligned with $\theta = 0$ is shown in Fig. 6.8. The deviatoric stress results in compression on the wellbore wall $\sigma_{\theta \theta} = 3 \Delta \sigma$ at $\theta = \pi/2$ and $3\pi/2$, and in tension $\sigma_{\theta \theta} = - \Delta \sigma$ at $\theta = 0$ and $\pi$. Hence, the presence of the wellbore amplifies compressive stresses 3 times $\sigma_{\theta \theta}/\sigma_{\infty}=3$ at $\theta = \pi/2$ and $3\pi/2$. The variation of stresses around the wellbore depend on harmonic functions $\sin (\theta)$ and $\cos (\theta)$.

   Figure 6.8: Kirsch solution for far-field deviatoric stress $\Delta \sigma$.

   

4. Pore pressure: The last step consists in assuming a perfect mud-cake, so that, the effective stress wall support (as shown in Fig. 6.7) is $(P_W - P_p)$ instead of $P_W$.

6.2.3 Complete Kirsch solution

Consider a vertical wellbore subjected to horizontal stresses $S_{Hmax}$ and $S_{hmin}$, both principal stresses, vertical stress $S_v$, pore pressure $P_p$, and wellbore pressure $P_W$. The corresponding effective in-situ stresses are $\sigma_{Hmax}$, $\sigma_{hmin}$, and $\sigma _v$. The Kirsch solution for a wellbore with radius $a$ within a linear elastic and isotropic solid is:

$$\left\lbrace \begin{array}{rcl} \sigma_{rr} & = & (P_W - P_p)... ...left( \frac{a^2}{r^2} \right) \cos (2\theta) \end{array}\right.$$ (6.2)

where $\sigma _{rr}$ is the radial effective stress, $\sigma _{\theta \theta }$ is the tangential (hoop) effective stress, $\sigma _{r\theta }$ is the shear stress in a plane perpendicular to $r$ in tangential direction $\theta$, and $\sigma_{zz}$ is the vertical effective stress in direction $z$. The angle $\theta$ is the angle between the direction of $S_{Hmax}$ and the point at which stress is considered. The distance $r$ is measured from the center of the wellbore. For example, at the wellbore wall $r=a$.

An example of the solution of Kirsch equations for $S_{Hmax}=22$ MPa, $S_{hmin}=13$ MPa, and $P_W=P_p=10$ MPa is available in Figure 6.9. The plots show radial $\sigma _{rr}$ and tangential $\sigma _{\theta \theta }$ effective stresses, as well as the calculated principal stresses $\sigma _3$ and $\sigma_{1}$.

Figure 6.9: Example of solution of Kirsch equations. The effective radial stress at the wellbore wall is $P_W-P_p = 0$. Top: solution for radial $\sigma _{rr}$ and hoop $\sigma _{\theta \theta }$ stresses. Bottom: solution for principal stresses (eigenvalues from $\sigma _{\theta \theta }$, $\sigma _{rr}$, and $\sigma _{r\theta }$ ). Notice that $\sigma _1$ is the highest at top and bottom and $\sigma _3$ is the lowest at the sides. The influence of the cavity extend to a few wellbore radii.

Let us obtain $\sigma _{rr}$ and $\sigma _{\theta \theta }$ at the wellbore wall $r=a$. The radial stress for all $\theta$ is

$$\sigma_{rr}(r=a) = P_W - P_p$$ (6.3)

The hoop stress depends on $\theta$,

$$\sigma_{\theta \theta} (r=a) = -(P_W - P_p) +(\sigma_{Hmax}+\sigma_{hmin}) -2(\sigma_{Hmax}-\sigma_{hmin}) \cos (2\theta)$$ (6.4)

and it is the minimum at $\theta = 0$ and $\pi$ (azimuth of $S_{Hmax}$) and the maximum at $\theta = \pi/2$ and $3\pi/2$ (azimuth of $S_{hmin}$):

$$\left\lbrace \begin{array}{rcl} \sigma_{\theta \theta} (r=a,\... ..._W - P_p) +3 \: \sigma_{Hmax} -\sigma_{hmin} \end{array}\right.$$ (6.5)

These locations will be prone to develop tensile fractures ( $\theta = 0$ and $\pi$) and shear fractures ( $\theta = \pi/2$ and $3\pi/2$). The shear stress around the wellbore wall is $\sigma_{r \theta} = 0$. This makes sense because fluids (drilling mud) cannot apply steady shear stresses on the surface of a solid. Finally, the effective vertical stress is

$$\sigma_{zz} (r=a) = \sigma_v - 2\nu (\sigma_{Hmax}-\sigma_{hmin}) \cos (2\theta)$$ (6.6)

6.3 Shear failure and wellbore breakouts

Wellbore breakouts are a type of rock failure around the wellbore wall and occur when the stress anisotropy $\sigma_1/\sigma_3$ surpasses the shear strength limit of the rock. Maximum anisotropy is found at $\theta = \pi/2$ and $3\pi/2$, for which

$$\left\lbrace \begin{array}{rcl} \sigma_1 = \sigma_{\theta \th... ...\\ \sigma_3 = \sigma_{rr} & = & (P_W - P_p) \end{array}\right.$$ (6.7)

Figure 6.10: Wellbore pressure for initiation of wellbore breakouts. Shear fractures will develop if $P_W < P_{Wshear}$.

Hence, replacing $\sigma _1$ and $\sigma _3$ into a shear failure equation (Eq. ) permits finding the mud pressure $P_{Wshear}$ that would produce a tiny shear failure (or breakout) at $\theta = \pi/2$ and $3\pi/2$:

$$\left[ -(P_W - P_p) +3 \: \sigma_{Hmax} -\sigma_{hmin} \right] = UCS + q \left[ P_W - P_p \right]$$ (6.8)

Hence,

$$P_{Wshear} = P_p + \frac{3\sigma_{Hmax} -\sigma_{hmin} - UCS}{1+q}$$ (6.9)

Mud pressure $P_W < P_{Wshear}$ would extend rock failure and breakouts further in the neighborhood of $\theta = \pi/2$ and $3\pi/2$ (See Fig. 6.11). Thus, $P_{Wshear}$ is the lowest mud pressure before initiation of breakouts.

Figure 6.11: Example of wellbore breakout [Zoback 2013 - Fig. 6.15]. Observe the inclination of shear fractures as the propagate into the rock. The material that falls into the wellbore is taken out as drilling cuttings.

PROBLEM 6.1: Calculate the minimum mud weight (ppg) in a vertical wellbore for avoiding shear failure (breakouts) in a site onshore at 7,000 ft of depth where $S_{hmin} =$ 4,300 psi and $S_{Hmax} =$ 6,300 psi and with hydrostatic pore pressure. The rock mechanical properties are $UCS =$ 3,500 psi, $\mu_i=$ 0.6, and $T_s$ = 800 psi.

SOLUTION
Hydrostatic pore pressure results in:

$$P_p = 7000$$    ft$$\times 0.44$$    psi/ft$$= 3080$$    psi

The effective horizontal stresses are:

$$\sigma_{Hmax} = 6300$$    psi$$- 3080$$    psi$$= 3220$$    psi$$$$

and

$$\sigma_{hmin} = 4300$$    psi$$- 3080$$    psi$$= 1220$$    psi$$$$

The friction angle is $\arctan(0.6)=30.96^{\circ}$, and therefore, the friction coefficient $q$ is

$$q = \frac{1+ \sin 30.96^{\circ} }{1- \sin 30.96^{\circ} } = 3.12$$

Thus, the minimum mud pressure for avoiding shear failure (breakouts) is

$$P_{Wshear} = 3080$$    psi$$+ \frac{3 \times 3220 \text{ psi} - 1220 \text{ psi} - 3500 \text{ psi} }{1+3.12} = 4279 \text{ psi}$$

This pressure can be achieved with an equivalent circulation density of

$$\frac{4279 \text{ psi}} {7000 \text{ ft}} \times \frac{8.3 \text{ ppg}} {0.44 \text{ psi/ft}} = 11.57 \text{ ppg} \: \: \blacksquare$$

6.3.1 Breakout angle determination

For a given set of problem variables (far field stress, pore pressure, and mud pressure), we can calculate the required strength of the rock to have a stable wellbore. Let us consider the example of Fig. 6.12 that shows the required $UCS$ to resist shear failure assuming the friction angle is $\varphi = 30^{\circ}$. For example, if the rock had a $UCS \sim 25$ MPa, one may expect a $\sim 90^{\circ}$ wide breakout in Fig. 6.12.

Figure 6.12: Example of required $UCS$ with Mohr-Coulomb analysis to verify likelihood of wellbore breakouts.

Alternatively, you could solve the previous problem analytically. The procedure consists in setting shear failure at the point in the wellbore at an angle $(w_{BO}/2)$ from $\pi/2$ or $3\pi/2$. Hence, at a point on the wellbore wall at $\theta_B = \pi/2 - w_{BO}/2$:

$$\left\lbrace \begin{array}{rcl} \sigma_{\theta \theta} & = & ... ...\theta_B) \\ \sigma_{rr} & = & +(P_W - P_p) \end{array}\right.$$ (6.10)

Figure 6.13: Determination of breakout angle with Mohr-Coulomb failure criterion.

Say hoop stress reaches the maximum principal stress anisotropy allowed by the Mohr-Coulomb shear failure criterion ( $\sigma_1 = UCS + q \: \sigma_3$) where the breakout begins (rock about to fail - Fig. 6.13), then

$$\left[ -(P_W - P_p) + (\sigma_{Hmax} + \sigma_{hmin}) - 2(\sigma_{Hmax} - \sigma_{hmin}) \cos (2 \theta_B) \right] = UCS + q (P_W - P_p)$$ (6.11)

which after some algebraic manipulations results in:

$$2 \theta_B = \arccos \left[ \frac{ \sigma_{Hmax} + \sigma_{hmin} - UCS - (1+q)(P_W - P_p)}{2(\sigma_{Hmax} - \sigma_{hmin})} \right]$$ (6.12)

The breakout angle is

$$w_{BO} = \pi - 2 \theta_B$$ (6.13)

The procedure assumes the rock in the breakout (likely already gone) is still resisting hoop stresses and therefore it is not accurate for large breakouts ( $w_{BO} \gtrsim 60^{\circ}$).

You could also calculate the wellbore pressure for a predetermined breakout angle by rearranging Eq. 6.12 to

$$P_{WBO} = P_p + \frac{ (\sigma_{Hmax} + \sigma_{hmin}) - 2(\sigma_{Hmax} - \sigma_{hmin}) \cos (\pi - w_{BO}) - UCS}{1+q}$$ (6.14)

PROBLEM 6.2: Calculate the breakout angle in a vertical wellbore for a mud weight of 10 ppg in a site onshore at 7,000 ft of depth where $S_{hmin} =$ 4,300 psi and $S_{Hmax} =$ 6,300 psi and with hydrostatic pore pressure. The rock mechanical properties are $UCS =$ 3,500 psi, $\mu_i=$ 0.6, and $T_s$ = 800 psi.

SOLUTION
The problem variables are the same of Problem 6.1. For a 10 ppg mud, the resulting mud pressure is

$$10$$    ppg$$\times \frac{0.44 \text{ psi/ft}} {8.3 \text{ ppg}} \times 7000 \text{ ft} = 3710 \text{ psi}$$

Hence, the expected wellbore breakout angle is

$$w_{BO} = 180^{\circ} - \arccos \left[ \frac{ 3220 \text{ psi} + 1... ...3220 \text{ psi} - 1220 \text{ psi})} \right] = 66 ^{\circ} \: \: \blacksquare$$

6.3.2 Breakout measurement

Breakouts and tensile induced fractures (Section 6.4) can be identified and measured with borehole imaging tools (Fig. 6.14). Breakouts appear as wide bands of longer travel time or higher electrical resistivity in borehole images. Tensile fractures appear as narrow stripes of longer travel time or higher electrical resistivity. Borehole images also permit identifying the direction of the stresses that caused such breakouts or tensile induced fractures. For example, the azimuth of breakouts coincides with the direction of $S_{hmin}$ in vertical wells.

Figure 6.14: Examples of wellbore breakouts and tensile fractures in borehole images. Learn more about wellbore imaging tools here: http://petrowiki.org/Borehole_imaging.

Breakouts can also be detected from caliper measurements. Caliper tools permit measuring directly the size and shape of the borehole (https://petrowiki.org/Openhole_caliper_logs). Thus, the caliper log is extremely useful to measure breakouts and extended breakouts (washouts). For the same mud density, the caliper log reflects changes of rock properties along the well and correlate with other well logging measurements.

6.3.3 Maximum horizontal stress determination from breakout angle

Breakouts are a consequence of stress anisotropy in the plane perpendicular to the wellbore. Hence, knowing the size and orientation of breakouts permits measuring and calculating the direction and magnitude of stresses that caused such breakouts. This technique is very useful for measuring orientation of horizontal stresses. In addition, if we know the rock properties $UCS$ and $q$, then it is possible to calculate the maximum principal stress in the plane perpendicular to the wellbore. For example, for a vertical wellbore the total maximum horizontal stress would be

$$S_{Hmax} = P_p + \frac{UCS + (1+q)(P_W - P_p) - \sigma_{hmin} \left[ 1 + 2 \cos (\pi - w_{BO}) \right]} {1 - 2 \cos (\pi - w_{BO})}$$ (6.15)

6.4 Tensile fractures and wellbore breakdown

Wellbore tensile (or open mode) fractures occur when the minimum principal stress $\sigma _3$ on the wellbore wall goes below the limit for tensile stress: the tensile strength $T_s$. Unconsolidated sands have no tensile strength. Hence, an open-mode fracture occurs early after effective stress goes to zero. The minimum hoop stress is located on the wall of the wellbore $(r=a)$ and at $\theta = 0$ and $\pi$ (Fig. 6.15):

$$\sigma_{\theta \theta} = -(P_W - P_p) -\sigma_{Hmax} + 3 \sigma_{hmin} + \sigma^{\Delta T}$$ (6.16)

Notice that we have added a temperature term $\sigma^{\Delta T}$ that takes into account wellbore cooling, an important phenomenon that contributes to tensile fractures in wellbores.

Figure 6.15: Occurrence of tensile fractures around a vertical wellbore. Tensile fractures will occur when $P_W > P_b$.

Matching the lowest value of hoop stress $\sigma _{\theta \theta }$ with tensile strength $T_s$ permits finding the mud pressure $P_W = P_{b}$ that would produce a tensile (or open mode) fracture:

$$-T_s = -(P_b - P_p) -\sigma_{Hmax} + 3 \sigma_{hmin} + \sigma^{\Delta T}$$ (6.17)

and therefore

$$P_b = P_p - \sigma_{Hmax} + 3 \sigma_{hmin} + T_s + \sigma^{\Delta T}$$ (6.18)

The subscript $b$ of $P_b$ corresponds to “breakdown” pressure because in some cases when $P_b > S_3$, a mud pressure $P_W > P_b$ can create a hydraulic fracture that propagates far from the wellbore and causes lost circulation during drilling. When $P_b < S_3$ and $P_W > P_b$, the mud pressure will produce short tensile fractures around the wellbore that do not propagate far from the wellbore.

In the equations above we have added the contribution of thermal stresses $\sigma^{\Delta T} = [\alpha_T E/(1-\nu)] \Delta T$ where $\alpha_T$ is the linear thermal expansion coefficient and $\Delta T$ is the change in temperature ( $\sigma^{\Delta T}<0$ for $\Delta T < 0$). Wellbores are usually drilled and logged with drilling mud cooler than the formation $T_{mud} < T_{rock}$. Cooling leads to solid shrinkage and stress relaxation (a reduction of compression stresses). Hence, ignoring thermal stresses is conservative for preventing breakouts but it is not for tensile fractures and should be taken into account when calculating $P_b$.

Fig. 6.16 shows an example of calculation of the local minimum principal stress $S_3$ around a wellbore. The locations with the lowest stress align with the direction of the far-field maximum stress in the plane perpendicular to wellbore axis.

Figure 6.16: Example of calculation of tensile strength required for wellbore stability. The figure shows that a tensile strength of $\sim 3$ MPa is required to avert tensile fractures in this example.

PROBLEM 6.3: Calculate the maximum mud weight (ppg) in a vertical wellbore for avoiding drilling-induced tensile fractures in a site onshore at 7,000 ft of depth where $S_{hmin} =$ 4,300 psi and $S_{Hmax} =$ 6,300 psi and with hydrostatic pore pressure. The rock mechanical properties are $UCS =$ 3,500 psi, $\mu_i=$ 0.6, and $T_s$ = 800 psi.

SOLUTION
The problem variables are the same of problem 6.1. The breakdown pressure $P_b$ in the absence of thermal effects is

$$P_b = 3080$$    psi$$- 3220$$    psi$$+ 3 \times 1220$$    psi$$+ 800$$    psi$$= 4320$$    psi

This pressure can be achieved with an equivalent circulation density of

$$\frac{4320 \text{ psi}} {7000 \text{ ft}} \times \frac{8.33 \text{ ppg}} {0.44 \text{ psi/ft}} = 11.68 \text{ ppg} \: \: \blacksquare$$

6.4.1 Identification of tensile fractures in wellbores

Similarly to breakouts, drilling-induced tensile fractures can be identified and measured with borehole imaging tools (Fig. 6.17). The azimuth of tensile fractures coincides with the direction of $S_{Hmax}$ in vertical wells.

Figure 6.17: Examples of drilling-induced tensile fractures along wellbores as seen with borehole imaging tools. Similarly to breakouts, tensile fractures can also help determine the orientation of the far field stresses.

6.5 The mud window

As seen in previous sections, low mud pressure (small mud wall support $\sigma _3$ for hoop stress $\sigma _1$) encourages shear failure while too much pressure encourages tensile fractures (well pressure adds tensile hoop stresses). Hence there is a range of mud pressure for which the wellbore will remain stable during drilling. This is called the mud window and has a lower bound (LB) and an upper bound (UB) which depend on wellbore mechanical stability as well as in other various technical requirements (Fig. 6.18).

Figure 6.18: Mud window based on mechanical wellbore stability, in-situ stresses, and pore pressure. HF: hydraulic fracture, LB: lower bound, and UB: upper bound.

Small breakouts $w_{BO} \leqslant 60^{\circ}$ may not compromise wellbore stability and permit setting a lower (more flexible) bound for the mud window. Large breakouts $w_{BO} \geqslant 120^{\circ}$ can lead to extensive shear failure and breakout growth which lead to stuck borehole assemblies and even wellbore collapse. Likewise, small drilling-induced tensile fractures with wellbore pressure $P_W$ lower than the minimum principal stress $S_3$ can be safe and extend the upper bound for the mud window. However, wellbore pressures above $S_3$ can result into uncontrolled mud-driven fracture propagation. Eq. 6.17 may suggest a safe breakdown pressure value above the minimum principal stress $P_b > S_3$. However, this calculation assumes tensile strength everywhere in the the borehole wall. Any rock flaw or fracture ($T_s = 0$ MPa) may reduce drastically $P_b$.

There are other factors to take into account in the determination of the mud window in addition to mechanical wellbore stability. First, a mud pressure below the pore pressure will induce fluid flow from the formation into the wellbore. The fluid flow rate will depend on the permeability of the formation. Tight formations may be drilled underbalanced with negligible production of formation fluid. High mud pressure with respect to the pore pressure will promote mud losses (by leak-off) and damage reservoir permeability. Second, a mud pressure above the far field minimum principal stress $S_3$ may cause uncontrolled hydraulic fracture propagation and lost circulation events during drilling.

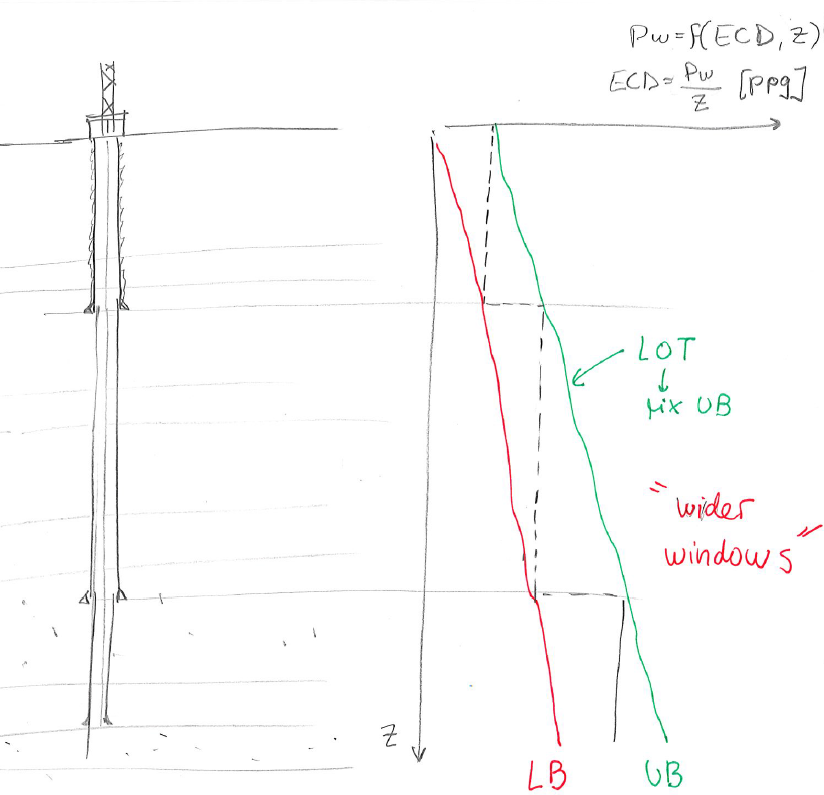
Maximizing the mud window (by taking advantage of geomechanical understanding among other variables) is extremely important to minimize the number of casing setting points and minimize drilling times (Fig. 6.19). The mud pressure gradient in a wellbore $\Delta P_W/ \Delta z$ is a constant and depends directly on the mud density. Therefore, drilling designs are based on the mud pressure with respect to a datum (usually the rotary Kelly bushing - RKB) expressed on terms of “equivalent density” to take into account viscous losses. In any open-hole section the value of pressure $P_W$ in a plot equivalent density v.s. depth is a straight vertical line (Fig. 6.2). The casing setting depth results from a selection of mud densities that cover the range between of the mud window as a function of depth. Wider mud windows reduce the number of casing setting points.

Figure 6.19: Drilling mud density and wellbore design. The drilling mud window depends on the lower and upper bounds (LB and UB) determined from geomechanical analysis. Careful geomechanical analysis favors “wider windows” and reduces the number of casing setting depths.

Managed pressure drilling consist in modifying the mud pressure at surface (positive or negative increase) or a certain control depth, such that there is one more control on wellbore pressure. The mud weight determines the gradient. The surface pressure control can offset the origin of the pressure hydrostatic “line”. Hence, these two controls can help adjust the pressure along the wellbore to fit in between lower and upper bounds better than just one control (mud weight).

Last, drastic changes in the mud window may happen whenever there is anomalous pore pressure, either too high or too low. Highly overpressured environments are challenging for drilling because of small effective stress and therefore small rock/sediment strength. The mechanisms for overpressure are discussed in Section 2.2. Anomalously low pressure decreases the least principal stress and is usually encountered when drilling through depleted formations that have not been recharged naturally. This topic is explored in Section 2.2.3 and thoroughly documented in a case study listed in Suggested Reading for this chapter.

6.6 Mechanical stability of deviated wellbores

The following subsections present a guide for calculating stresses at the wall of deviated wellbores and identifying stress magnitudes and locations for shear failure (breakouts) and tensile fractures.

6.6.1 Wellbore orientation

At any point along the trajectory of a deviated wellbore, the tangent orientation permits defining wellbore azimuth $\delta$ and deviation $\varphi$ (Fig. 6.20). Azimuth $\delta$ is the angle between the projection of the trajectory on a horizontal plane and the North. Deviation $\varphi$ is the angle between a vertical line and the trajectory line at the point of consideration. These two variables can be plotted in a half-hemisphere projection plot (stereonet). Notice that a point in this plot represents just one point along a wellbore trajectory. Fig. 6.20 shows an example of the full trajectory of a wellbore.

Figure 6.20: (a) Convention for plotting the orientation of a deviated wellbore on a lower hemisphere projection. (b) The example shows the deviation survey for a real wellbore (deviation range amplified to highlight small deviations). Notice that it starts slightly deviated on surface and then turns into vertical direction at depth.

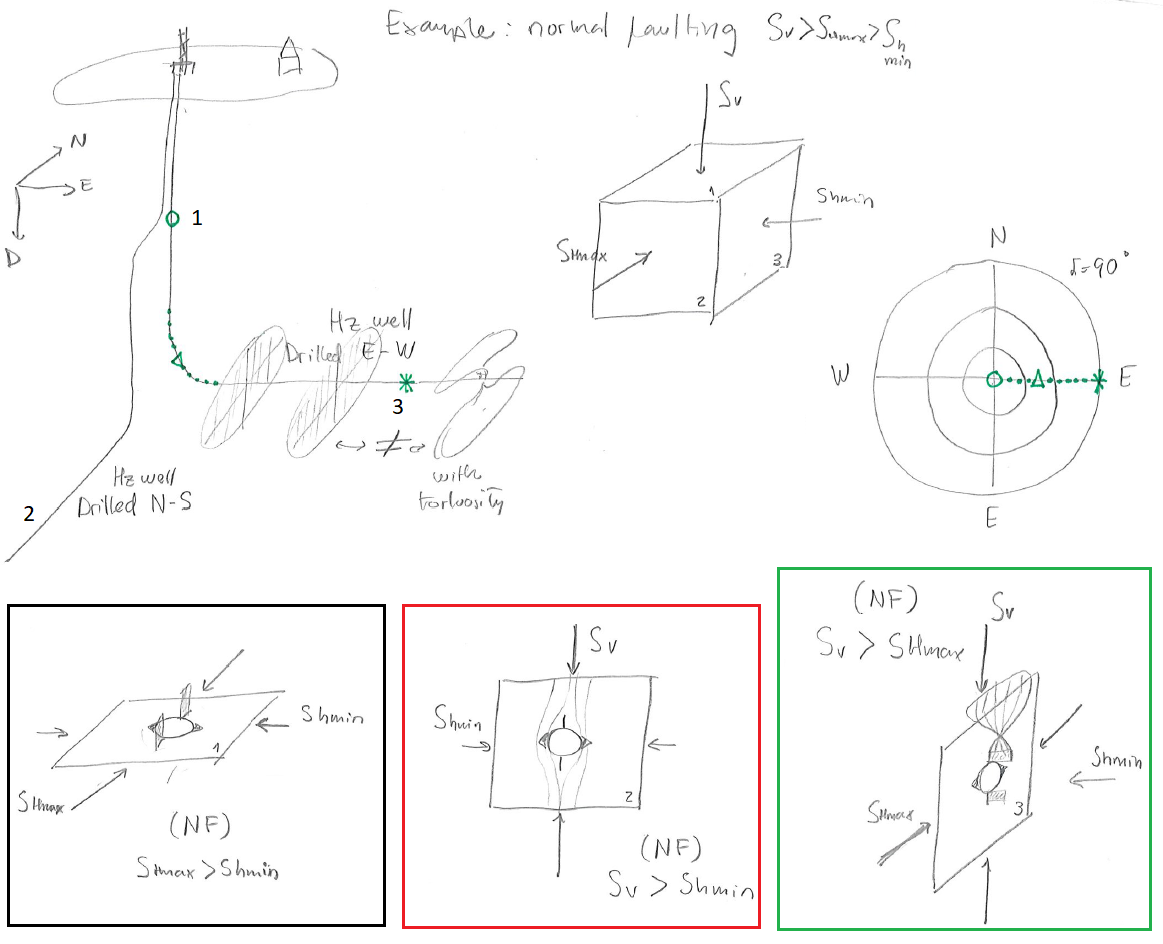
A given state of stress will result in different mud windows and locations of rock failure depending on the wellbore orientation. Breakouts and tensile fractures will depend on the stresses on the plane perpendicular to the wellbore. Figure 6.21 shows an example for normal faulting with generic stress magnitude values.

Figure 6.21: Example of expected location of wellbore breakouts and tensile fractures in a vertical and horizontal wellbores according to the state of stress (normal faulting with $S_{Hmax}$ in N-S direction here).

PROBLEM 6.4: Consider a place where vertical stress $S_v$ is a principal stress and the maximum horizontal stress acts in E-W direction.

1. Find the planes with maximum stress anisotropy for normal faulting, strike-slip, and reverse faulting stress regimes.
2. Plot the orientation of wellbores in those planes of maximum stress anisotropy in a stereonet projection plot.
3. Where around the wellbore would breakouts and tensile fractures occur in each case?

SOLUTION
The solution below shows just one of the possible solutions of two horizontal wells.

6.6.2 Calculation of stresses on deviated wellbores

Let us define a coordinate system for a point along the trajectory of a deviated wellbore. The first element $x_b$ of the cartesian base goes from the center of a cross-section of the wellbore at a given depth to the deepest point around the cross-section (perpendicular to the axis). The second element of the base $y_b$ goes from the center to the side on a horizontal plane. The third element of the base $z_b$ goes along the direction of the wellbore.

Figure 6.22: The wellbore coordinate system.

Based on the previous definition, it is possible to construct a transformation matrix $R_{GW}=f(\delta,\varphi)$ that links the geographical coordinate system and the wellbore coordinate system.

$$\uuline{S}{}_W = R_{GW} \uuline{S}{}_G R_{GW}^T$$ (6.19)

Furthermore, the wellbore stresses can be calculated from the principal stress tensor according with:

$$\uuline{S}{}_W = R_{GW} R_{PG}^T \uuline{S}{}_P R_{PG} R_{GW}^T$$ (6.20)

Where $\uuline{S}{}_P$ and $R_{PG}$ are the principal stress tensor and the corresponding change of coordinate matrix to the geographical coordinate system (Eq. 5.7). The tensor $\uuline{S}{}_W$ is composed by the following stresses:

$$\uuline{S}{}_W = \left[ \begin{array}{ccc} S_{11} & S_{12} & ... ...2} & S_{23} \\ S_{31} & S_{32} & S_{33} \\ \end{array}\right]$$ (6.21)

Stresses on the plane of the cross-section of the deviated wellbore at the wellbore wall $(\sigma_{rr}, \sigma_{\theta \theta}, \sigma_{zz}, \sigma_{\theta z})$ depend on far-field stresses $\sigma_{11} = S_{11} - P_p$, $\sigma_{22} = S_{22} - P_p$, $\sigma_{33} = S_{33} - P_p$, $\sigma_{12} = S_{12}$, $\sigma_{13} = S_{13}$, and $\sigma_{23} = S_{23}$. The Kirsch equations require additional far field shear terms $\sigma_{12}$, $\sigma_{13}$, and $\sigma_{23}$ in order to account for principal stresses not coinciding with the wellbore orientation. The solution of Kirsch equation for isotropic rock with far-field shear stresses is provided in Fig. 6.23.

Figure 6.23: Stresses around the wall of a deviated wellbore. Notice that principal stresses (directions $(x_1,x_2,x_3)$) may not be aligned with the wellbore trajectory.

Solving for the local principal stresses $(\sigma_{tmax}, \sigma_{rr}, \sigma_{tmin})$ on the wellbore wall permits checking for rock failure (tensile or shear). The local principal stresses may not be necessarily aligned with the wellbore axis leading to an angle $\omega$ (see Fig. 6.24). Because of such angle, tensile fractures in deviated wellbores can occur at an angle $\omega$ from the axis of the wellbore and appear as a series of short inclined (en-échelon) fractures instead of a long tensile fracture parallel to the wellbore axis as in Fig. 6.17.

Figure 6.24: Principal stresses around the wall of a deviated wellbore. The hoop stress $\sigma _{\theta \theta }$ could be the least, the intermediate or the maximum principal stress depending on location (angle $\theta$).

6.6.3 Breakout analysis for deviated wellbores

Consider a place subjected to strike-slip stress regime with $S_{Hmax}$ oriented at an azimuth of 070$^{\circ }$ with known values of principal stresses (Fig 6.25). The maximum stress anisotropy lies in a plane that contains $S_1 = S_{Hmax}$ and $S_3 = S_{hmin}$, a plane perpendicular to the axis of a vertical wellbore. Hence, maximum stress amplification at the wellbore wall will happen for a vertical wellbore. The minimum stress anisotropy lies in a plane that contains $S_2 = S_{v}$ and $S_3 = S_{hmin}$, perpendicular to a horizontal wellbore drilled in direction of $S_{Hmax}$. Given a mud pressure and a fixed friction angle, we can calculate for a given wellbore orientation the stresses on the wellbore wall from equations in Fig. 6.24, and the required $UCS$ (using a shear failure criterion $\sigma_1 = UCS + q \: \sigma_3$) to avert shear failure. The plots in Fig. 6.25 are examples of this calculation. The maximum value of required $UCS$ corresponds to the wellbore direction with maximum stress anisotropy (vertical wellbore - red region), and the minimum value of required $UCS$ corresponds to the wellbore direction with minimum stress anisotropy (horizontal wellbore with $\delta = 070^{\circ}$ - blue region). Following the breakout concepts discussed before, we would expect breakouts at 160$^{\circ }$ and 340$^{\circ }$ of azimuth on the sides of a vertical wellbore. A horizontal wellbore drilled in the direction of $S_{hmin}$ would tend to develop breakouts on the top and bottom of the wellbore.

Figure 6.25: Stereonet plots to verify the rock strength required to avoid breakouts and the wellbore breakout angle for a given rock strength and wellbore pressure.

PROBLEM 6.5: Consider a place with principal stresses $S_v = 70$ MPa, $S_{Hmax} = 67$ MPa (at 070$^{\circ }$), $S_{hmin} = 45$ MPa, $P_p = 32$ MPa, and $P_W = 32$ MPa. Calculate the required UCS using the Coulomb failure criterion (with $\mu_i = 0.8$) for all possible wellbore orientations. Plot results in a stereonet projection.

SOLUTION

PROBLEM 6.6: Consider a place with principal stresses $S_v = 70$ MPa, $S_{Hmax} = 105$ MPa (at 070$^{\circ }$), $S_{hmin} = 85$ MPa, $P_p = 32$ MPa, and $P_W = 32$ MPa. Calculate the required UCS using the Coulomb failure criterion (with $\mu_i = 0.8$) for all possible wellbore orientations. Plot results in a stereonet projection.

SOLUTION

A general workflow or algorithm to calculate mechanical failure for all possible wellbore deviations is the following:

1. Calculate the stress tensor in the geographical coordinate system: $S_G$, given principal stresses $S_P$ and principal stress directions $(\alpha, \gamma, \beta)$.
2. Begin a for loop (say counter $i$), to explore deviation angle from 0 to 90 degrees.
   1. Within this first loop, open a second loop (say counter $j$) to explore azimuth from 0 to 360 degrees.
   2. For each deviation and azimuth $(i,j)$, calculate stresses in the wellbore coordinate system $S_W$, a function of $R_{GW}$.
   3. For each deviation and azimuth $(i,j)$, open a third loop (say counter $k$), to calculate stress at and around the wellbore wall for a cross section with angle from 0 to 360 degrees.
      1. At each point around the well, calculate stresses and get principal stresses.
      2. For each point along the well, use the principal stresses to predict whether there is failure or not, and what type.
      3. Save all this failure yes/no/type data
   4. After checking failure around the well (out of counter $k$), analyze this data to output a quantity for each orientation ($i,j$). For example, you could count how many points are failing in shear and get from here the breakout angle.
3. Summarize all your results with a polar projection/stereonet plot.

6.6.4 Tensile fractures analysis for deviated wellbores

The procedure to find tensile failure is equivalent to the one used for shear failure, but using a tensile strength failure criterion. For example, consider a place subjected to normal faulting stress regime with $S_{Hmax}$ oriented at an azimuth of 070$^{\circ }$ and known values of principal stresses (Fig. 6.26). The maximum stress anisotropy lies in a plane that contains $S_1 = S_{v}$ and $S_3 = S_{hmin}$, perpendicular to a horizontal wellbore drilled in the direction of $S_{Hmax}$. For a given rock tensile strength, we can calculate the maximum mud pressure that the wellbore can bear without failing in tension. Fig. 6.26 shows an example of this calculation. The maximum possible $P_W$ corresponds to the wellbore direction with minimum stress anisotropy (blue region), and the minimum possible $P_W$ corresponds to the wellbore direction with maximum stress anisotropy (red region). For example, tensile fractures would tend to occur in the top and bottom of a horizontal wellbore drilled in the direction of $S_{Hmax}$.

Figure 6.26: Calculation of required $T_S$ as a function of wellbore orientation in order to prevent open-mode fractures with $P_W = 35$ MPa. Stresses and pore pressure: $S_v =$ 70 MPa, $S_{Hmax} =$ 55 MPa, $S_{hmin} =$ 45 MPa, and $P_p =$ 32 MPa, Notice that the stress regimes dictates the orientation of the least and most convenient drilling direction.

PROBLEM 6.7: Consider a place with principal stresses $S_v = 70$ MPa, $S_{Hmax} = 105$ MPa (at 070$^{\circ }$), $S_{hmin} = 55$ MPa, and $P_p = 32$ MPa. Calculate the maximum wellbore pressure $P_W$ at the limit of tensile strength with $T_s = 0$ MPa) for all possible wellbore orientations. Plot results in a stereonet projection.

SOLUTION
TBD

PROBLEM 6.8: Consider a place with principal stresses $S_v = 70$ MPa, $S_{Hmax} = 105$ MPa (at 070$^{\circ }$), $S_{hmin} = 85$ MPa, and $P_p = 32$ MPa. Calculate the maximum wellbore pressure $P_W$ at the limit of tensile strength with $T_s = 0$ MPa) for all possible wellbore orientations. Plot results in a stereonet projection.

SOLUTION
TBD

6.7 Thermal, chemical, and leak-off effects on wellbore stability

Wellbore stability is affected by various factors other than far-field stresses and mud pressure. Some of the most important factors include: changes of temperature, changes of salinity in the resident brine within the pore space in the rock, and changes of pore pressure near the wellbore wall.

6.7.1 Thermal effects

Drilling mud is usually cooler than the geological formations in the subsurface. Because of such difference, drilling mud usually lowers the temperature of the rock near the wellbore. The process is time dependent and variations of temperature $T$ in time and space (in the absence of fluid flow) can be modeled using the heat diffusivity equation:

$$\frac{\partial T}{\partial t} = D_T \nabla^2 T$$ (6.22)

where heat diffusivity is $D_T = k_T/(\rho c_p)$ proportional to the heat conductivity $k_T$, and inversely proportional to the rock mass density $\rho$ and the heat capacity $c_p$. The operator $\nabla^2=(\partial^2 / \partial x^2 + \partial^2 / \partial y^2 + \partial^2 / \partial z^2 )$ indicates variations in space. The heat diffusivity equation and the equations of thermo-elasticity (Section 3.7.2) permit solving the changes of strains and stresses around the wellbore due to time-dependent changes of temperature.

Figure 6.27: Cooling $T<T_0$ leads to stress relaxation and possibly tensile stresses on the wellbore wall.

At steady-state conditions, the change in hoop stress $\Delta \sigma_{\theta \theta}$ around any point on the wellbore wall due to a change in temperature $\Delta T$ is:

$$\Delta \sigma_{\theta \theta} = \frac{\alpha_L E \Delta T}{1-\nu}$$ (6.23)

where $\alpha_L$ is the linear thermal expansion coefficient. Cooling leads to hoop stress relaxation and possibly tensile effective stress, while heating leads to increased compression in the tangential direction.

6.7.2 Chemo-electrical effects

Chemo-electrical effects are most relevant to small sub-micron particles, such as clays, the building-blocks of mudrocks and shales. The forces that act on clay particles include (Figure 6.28):

• Mechanical forces: solid skeletal stress and pore pressure,
• Electrical forces: van der Waals attraction, Born repulsion, short range repulsive and attractive forces induced by hydration/solvation of clay surfaces.

Figure 6.28: Schematic of clay platelet pair, forces between them, and equilibrium interparticle distance $d$.

Shale chemical instability involves changes of the electrical forces between clay platelets due to changes of ionic concentration of the resident brine within the rock pore space. The equilibrium distance between particles is inversely proportional to salinity. Hence, decreasing salinity promotes chemo-electrical swelling of shale (see example in Fig. 6.29). During drilling, the change in ionic concentration in resident brine is caused by leak-off of low-salinity water from drilling mud into the formation saturated with high salinity brine. Smectite clays are most sensitive to swelling upon water freshening and hydration.

Figure 6.29: Example of shale hydration and swelling due to exposure to low salinity water.

Shale swelling leads to an increase of hoop stress and sometimes rock weakening around the wellbore wall. Such changes promote shear failure and breakouts/washouts (Fig. 6.30). Prevention of shale chemical instability requires modeling of solute diffusive-advective transport between the drilling mud and the formation water in the rock. Higher mud pressures result in higher leak-off, and therefore, in more rapid ionic exchange within the shale. The process is time-dependent. Thus, the expected break out angle results from a combination of mechanical factors (stresses around the wellbore) and shale sensitivity to low salinity muds.

Figure 6.30: Shale sensitivity: variation of near wellbore stresses and time-dependent breakout angle $w_{BO}$ prediction example.

The solutions to wellbore instability problems due to shale chemo-electrical swelling are: increasing the salinity of water-based drilling muds, using oil-based muds instead of water-based muds, cooling the wellbore to counteract increases of hoop stress, and using underbalanced-drilling to minimize leak-off of water from drilling mud.

6.7.3 Leak-off effects

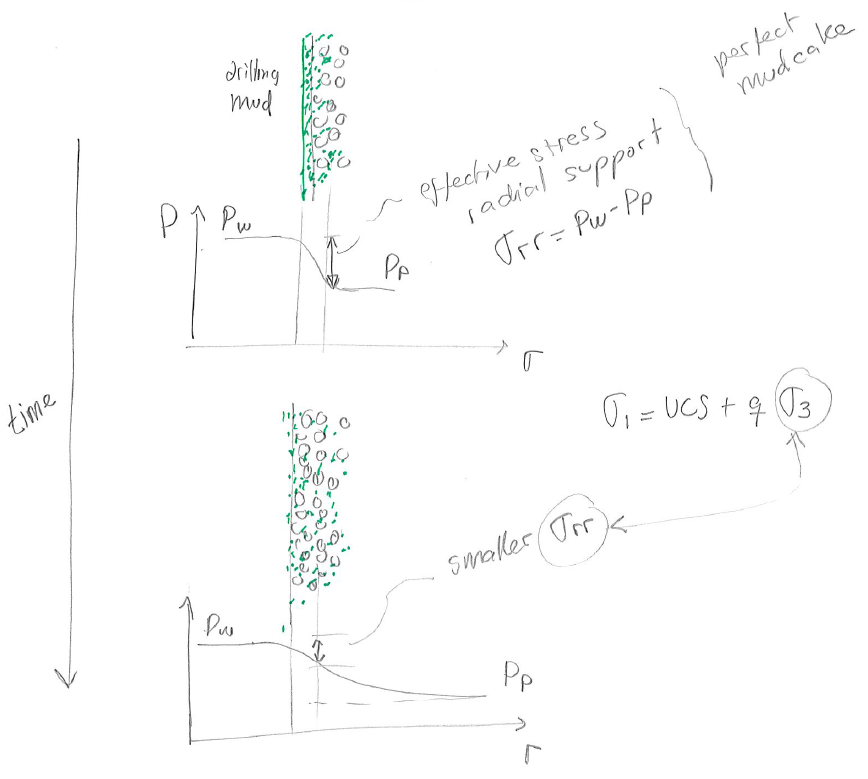
So far we have assumed that the radial effective stress at the wellbore wall is $\sigma_{rr} = P_W - P_p$. Such assumption implies a perfect and sharp “mudcake” that creates a sharp gradient between the mud pressure and the pore pressure, such that, viscous forces apply an effective stress $\sigma_{rr} = P_W - P_p$ on the wellbore wall (Fig. 6.4). However, mud water leak off and mud filtration can occur over time decreasing the sharpness of such gradient and reducing the effective stresses in the near wellbore region. A reduction of effective stress lowers the strength of rock and favors rock failure around the wellbore. Hence, a wellbore could be stable right after drilling, but unstable after some time due to mud filtration and loss of radial stress support.

Figure 6.31: Loss of mudcake after excessive particle filtration. The loss of mudcake leads to a decrease in effective stress radial support and therefore rock shear strength.

6.8 Strength anisotropy

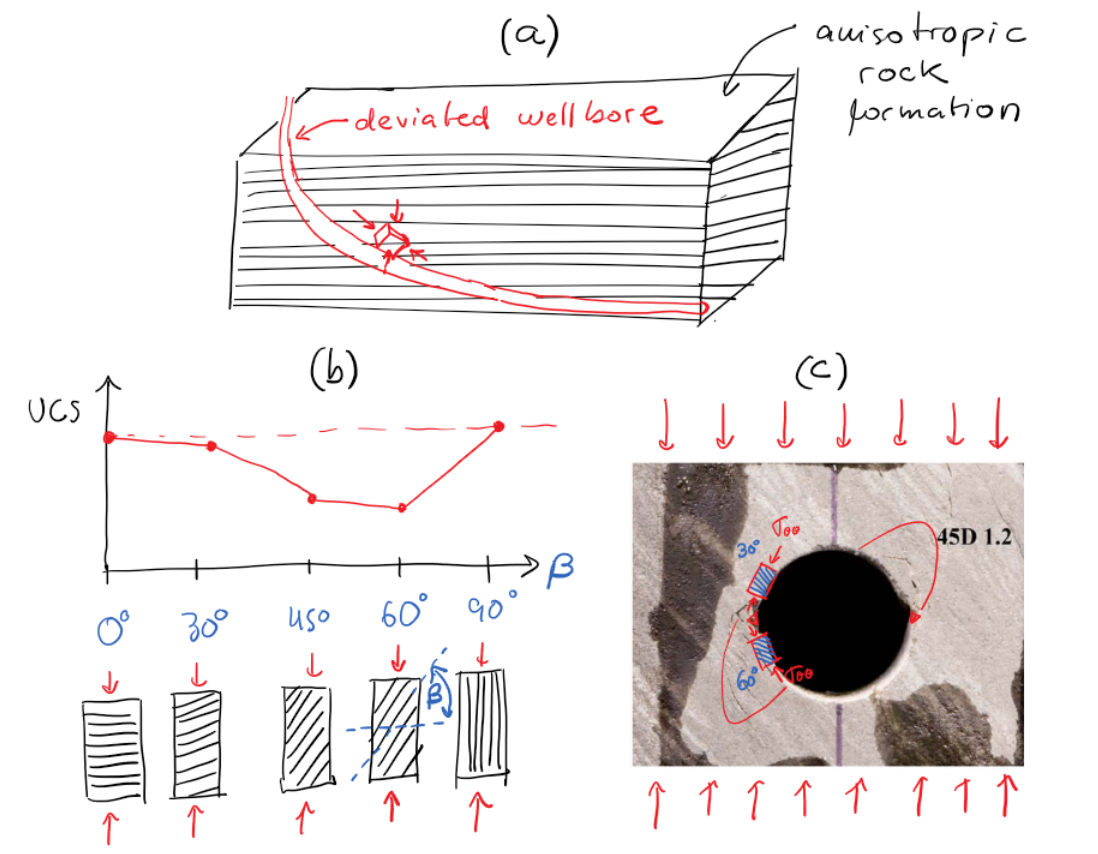
Sedimentary rocks are anisotropic. Rock lamination contributes to stiffness and strength anisotropy. Consider a deviated wellbore as in Fig. 6.32. Far field stress anisotropy will result in high stress anisotropy regions (red zone perpendicular to the direction of maximum stress) and potential breakouts if the strength of intact rock is overcome. Yet, there will be other areas around the wellbore without such high stress anisotropy but high enough and aligned optimally to induce shear failure in regions weakened by the presence of rock lamination (blue zone). Such areas may also be prone to develop a second family of breakouts.

Figure 6.32: Implications of rock strength anisotropy on wellbore breakouts. Credit for background image in (c): https://doi.org/10.1029/2018JB017090.

6.9 Problems

1. Using equations of stresses around a cylindrical cavity, calculate near-wellbore effective radial $\sigma _{rr}$ and hoop $\sigma _{\theta \theta }$ stresses for a vertical well 8 in diameter in the directions of $S_{hmin}$ (4,500 psi – acting E-W) and $S_{Hmax}$ (6,000 psi) up to 3 ft of distance considering that $P_p$ = 3200 psi and
   1. $P_W$ = 3,200 psi
   2. $P_W$ = 4,000 psi
   The result should be presented as plots of stresses ( $\sigma _{rr}$, $\sigma _{\theta \theta }$) for $\theta = 0$ and $\theta=90^{\circ}$ as a function of distance ($r \geq a$) from the center of the wellbore.

2. Effect of overpressure: Consider the problem solved in class (Wellbore: vertical; Site: onshore, 7,000 ft of depth, $S_v$ = 7,000 psi, $S_{hmin}$ = 4,300 psi, $S_{Hmax}$ = 6,300 psi; Rock properties: $UCS$ = 3,500 psi, $\mu = 0.6$, $T_s$ = 800 psi).
   1. Calculate wellbore pressure and corresponding mud weight for (i) $w_{BO}=70^{\circ}$, (ii) $w_{BO} \sim 0^{\circ}$ ( $P_{Wshear}$), and (iii) for inducing tensile fractures ($P_b$) for $\lambda_p= 0.52$ and $\lambda_p= 0.60$. Compare with $\lambda_p= 0.44$ solved in class. How does the drilling mud window change with varying pore pressure?
   2. Assume horizontal stress directions near Dallas-Fort Worth region. What would the azimuth of breakouts and drilling induced fractures be? https://www.nature.com/articles/s41467-020-15841-5/figures/1

3. Effect of stress anisotropy (differential stress) $(\sigma_{Hmax} - \sigma_{hmin})$: Consider the following problem, Wellbore: vertical; Site: onshore, 2 km of depth, $dS_v/dz = 23$ MPa/km, $\lambda_p= 0.44$, $\sigma_{hmin} = 0.4 \: \sigma_v$; Rock properties: $UCS$ = 7 MPa, $q=3.9$, $T_s$ = 2 MPa. Calculate wellbore pressure and corresponding mud weight for (i) $w_{BO}=45^{\circ}$, (ii) $w_{BO} \sim 0^{\circ}$, and (iii) for inducing tensile fractures for
   1. $\sigma_{Hmax} = 0.6 \: \sigma_v$
   2. $\sigma_{Hmax} = 0.8 \: \sigma_v$
   3. $\sigma_{Hmax} = 1.0 \: \sigma_v$
   4. How does the drilling mud window change with $(\sigma_{Hmax} - \sigma_{hmin})$?

4. Offshore: Consider an offshore vertical wellbore being drilled at 2 km of total vertical depth, with 500 m of water, hydrostatic pore pressure, $\sigma_{hmin} = 0.4 \: \sigma_v$, $\sigma_{Hmax} = 0.8 \: \sigma_v$. The rock properties are $UCS$ = 7 MPa, $q=3.9$, $T_s$ = 2 MPa. Calculate wellbore pressure and corresponding mud weight for (i) $w_{BO}=45^{\circ}$, (ii) $w_{BO} \sim 0^{\circ}$, and (iii) for inducing tensile fractures.

5. Horizontal wells: Evaluate wellbore stability for horizontal wells that you will need to exploit in a gas reservoir subjected to a strike-slip stress environment.
   1. Consider two wellbores: one drilled parallel to $S_{hmin}$ and another drilled parallel to $S_{Hmax}$. Draw cross-sections of these two wells, identify involved stresses, and clearly mark expected positions of tensile fractures and wellbore breakouts.
   2. The horizontal wells lie at about 8,000 ft depth where it is estimated that $S_{hmin}$ = 50 MPa, $S_{Hmax}$ = 70 MPa, $dS_v/dz = 1$ psi/ft and $\lambda_p=0.6$. The unconfined compressive strength of the rock is 8,500 psi, the rock internal friction coefficient is $\mu_i=1.0$, and tensile strength is about $T_s = 0$ psi given the large density of natural fractures. Determine the mechanical stability limits on wellbore pressure for both horizontal well directions considered. Assume a breakout angle $w_{BO}=70^{\circ}$ to calculate the lower bound for the mud window.
   3. Determine mud density window appropriate for these wells (keep in mind potential lost circulation).
   4. Which one appears to have a wider mud window? Justify

6.10 Further reading and references

1. Fjaer, E., Holt, R.M., Raaen, A.M., Risnes, R. and Horsrud, P., 2008. Petroleum related rock mechanics (Vol. 53). Elsevier. (Chapters 4 and 9)
2. Heggheim T. and J. Andrews, 2023, Learnings from Successful Drilling in Heavily Depleted HPHT Reservoir with Up to 460 Bar Depletion. IADC/SPE-212526-MS. https://doi.org/10.2118/212526-MS
3. Jaeger, J.C., Cook, N.G. and Zimmerman, R., 2009. Fundamentals of rock mechanics. John Wiley & Sons. (Chapter 8)
4. Zoback, M.D., 2010. Reservoir geomechanics. Cambridge University Press. (Chapters 6 and 8)