6.7 Thermal, chemical, and leak-off effects on wellbore stability

Wellbore stability is affected by various factors other than far-field stresses and mud pressure. Some of the most important factors include: changes of temperature, changes of salinity in the resident brine within the pore space in the rock, and changes of pore pressure near the wellbore wall.

6.7.1 Thermal effects

Drilling mud is usually cooler than the geological formations in the subsurface. Because of such difference, drilling mud usually lowers the temperature of the rock near the wellbore. The process is time dependent and variations of temperature $T$ in time and space (in the absence of fluid flow) can be modeled using the heat diffusivity equation:

$$\frac{\partial T}{\partial t} = D_T \nabla^2 T$$ (6.22)

where heat diffusivity is $D_T = k_T/(\rho c_p)$ proportional to the heat conductivity $k_T$, and inversely proportional to the rock mass density $\rho$ and the heat capacity $c_p$. The operator $\nabla^2=(\partial^2 / \partial x^2 + \partial^2 / \partial y^2 + \partial^2 / \partial z^2 )$ indicates variations in space. The heat diffusivity equation and the equations of thermo-elasticity (Section 3.7.2) permit solving the changes of strains and stresses around the wellbore due to time-dependent changes of temperature.

Figure 6.26: Cooling $T<T_0$ leads to stress relaxation and possibly tensile stresses on the wellbore wall.

At steady-state conditions, the change in hoop stress $\Delta \sigma_{\theta \theta}$ around any point on the wellbore wall due to a change in temperature $\Delta T$ is:

$$\Delta \sigma_{\theta \theta} = \frac{\alpha_L E \Delta T}{1-\nu}$$ (6.23)

where $\alpha_L$ is the linear thermal expansion coefficient. Cooling leads to hoop stress relaxation and possibly tensile effective stress, while heating leads to increased compression in the tangential direction.

6.7.2 Chemo-electrical effects

Chemo-electrical effects are most relevant to small sub-micron particles, such as clays, the building-blocks of mudrocks and shales. The forces that act on clay particles include (Figure 6.27):

• Mechanical forces: solid skeletal stress and pore pressure,
• Electrical forces: van der Waals attraction, Born repulsion, short range repulsive and attractive forces induced by hydration/solvation of clay surfaces.

Figure 6.27: Schematic of clay platelet pair, forces between them, and equilibrium interparticle distance $d$.

Shale chemical instability involves changes of the electrical forces between clay platelets due to changes of ionic concentration of the resident brine within the rock pore space. The equilibrium distance between particles is inversely proportional to salinity. Hence, decreasing salinity promotes chemo-electrical swelling of shale (see example in Fig. 6.28). During drilling, the change in ionic concentration in resident brine is caused by leak-off of low-salinity water from drilling mud into the formation saturated with high salinity brine. Smectite clays are most sensitive to swelling upon water freshening and hydration.

Figure 6.28: Example of shale hydration and swelling due to exposure to low salinity water.

Shale swelling leads to an increase of hoop stress and sometimes rock weakening around the wellbore wall. Such changes promote shear failure and breakouts/washouts (Fig. 6.29). Prevention of shale chemical instability requires modeling of solute diffusive-advective transport between the drilling mud and the formation water in the rock. Higher mud pressures result in higher leak-off, and therefore, in more rapid ionic exchange within the shale. The process is time-dependent. Thus, the expected break out angle results from a combination of mechanical factors (stresses around the wellbore) and shale sensitivity to low salinity muds.

Figure 6.29: Shale sensitivity: variation of near wellbore stresses and time-dependent breakout angle $w_{BO}$ prediction example.

The solutions to wellbore instability problems due to shale chemo-electrical swelling are: increasing the salinity of water-based drilling muds, using oil-based muds instead of water-based muds, cooling the wellbore to counteract increases of hoop stress, and using underbalanced-drilling to minimize leak-off of water from drilling mud.

6.7.3 Leak-off effects

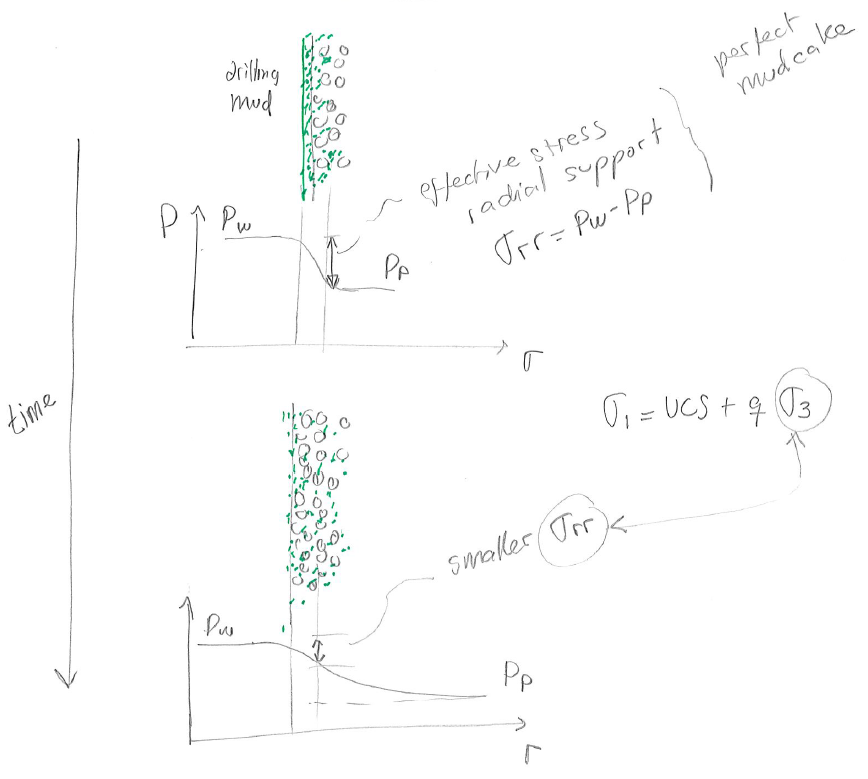
So far we have assumed that the radial effective stress at the wellbore wall is $\sigma_{rr} = P_W - P_p$. Such assumption implies a perfect and sharp “mudcake” that creates a sharp gradient between the mud pressure and the pore pressure, such that, viscous forces apply an effective stress $\sigma_{rr} = P_W - P_p$ on the wellbore wall (Fig. 6.3). However, mud water leak off and mud filtration can occur over time decreasing the sharpness of such gradient and reducing the effective stresses in the near wellbore region. A reduction of effective stress lowers the strength of rock and favors rock failure around the wellbore. Hence, a wellbore could be stable right after drilling, but unstable after some time due to mud filtration and loss of radial stress support.

Figure 6.30: Loss of mudcake after excessive particle filtration. The loss of mudcake leads to a decrease in effective stress radial support and therefore rock shear strength.