6.5 The mud window

As seen in previous sections, low mud pressure (small mud wall support $\sigma _3$ for hoop stress $\sigma _1$) encourages shear failure while too much pressure encourages tensile fractures (well pressure adds tensile hoop stresses). Hence there is a range of mud pressure for which the wellbore will remain stable during drilling. This is called the mud window and has a lower bound (LB) and an upper bound (UB) which depend on wellbore mechanical stability as well as in other various technical requirements (Fig. 6.17).

Figure 6.17: Mud window based on mechanical wellbore stability, in-situ stresses, and pore pressure. HF: hydraulic fracture, LB: lower bound, and UB: upper bound.

Small breakouts $w_{BO} \leqslant 60^{\circ}$ may not compromise wellbore stability and permit setting a lower (more flexible) bound for the mud window. Large breakouts $w_{BO} \geqslant 120^{\circ}$ can lead to extensive shear failure and breakout growth which lead to stuck borehole assemblies and even wellbore collapse. Likewise, small drilling-induced tensile fractures with wellbore pressure $P_W$ lower than the minimum principal stress $S_3$ can be safe and extend the upper bound for the mud window. However, wellbore pressures above $S_3$ can result into uncontrolled mud-driven fracture propagation. Eq. 6.17 may suggest a safe breakdown pressure value above the minimum principal stress $P_b > S_3$. However, this calculation assumes tensile strength everywhere in the the borehole wall. Any rock flaw or fracture ($T_s = 0$ MPa) may reduce drastically $P_b$.

There are other factors to take into account in the determination of the mud window in addition to mechanical wellbore stability. First, a mud pressure below the pore pressure will induce fluid flow from the formation into the wellbore. The fluid flow rate will depend on the permeability of the formation. Tight formations may be drilled underbalanced with negligible production of formation fluid. High mud pressure with respect to the pore pressure will promote mud losses (by leak-off) and damage reservoir permeability. Second, a mud pressure above the far field minimum principal stress $S_3$ may cause uncontrolled hydraulic fracture propagation and lost circulation events during drilling.

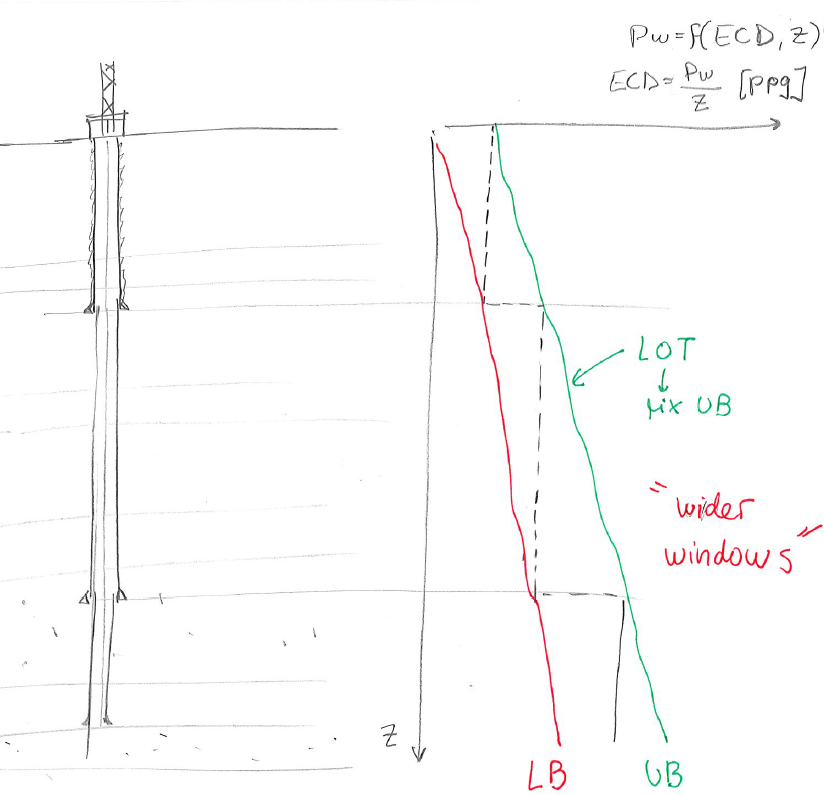
Maximizing the mud window (by taking advantage of geomechanical understanding among other variables) is extremely important to minimize the number of casing setting points and minimize drilling times (Fig. 6.18). The mud pressure gradient in a wellbore $\Delta P_W/ \Delta z$ is a constant and depends directly on the mud density. Therefore, drilling designs are based on the mud pressure with respect to a datum (usually the rotary Kelly bushing - RKB) expressed on terms of “equivalent density” to take into account viscous losses. In any open-hole section the value of pressure $P_W$ in a plot equivalent density v.s. depth is a straight vertical line (Fig. 6.2). The casing setting depth results from a selection of mud densities that cover the range between of the mud window as a function of depth. Wider mud windows reduce the number of casing setting points.

Figure 6.18: Drilling mud density and wellbore design. The drilling mud window depends on the lower and upper bounds (LB and UB) determined from geomechanical analysis. Careful geomechanical analysis favors “wider windows” and reduces the number of casing setting depths.

Managed pressure drilling consist in modifying the mud pressure at surface (positive or negative increase) or a certain control depth, such that there is one more control on wellbore pressure. The mud weight determines the gradient. The surface pressure control can offset the origin of the pressure hydrostatic “line”. Hence, these two controls can help adjust the pressure along the wellbore to fit in between lower and upper bounds better than just one control (mud weight).