8.1 Changes of stress in the reservoir rock

Reservoir depletion requires changes of pore pressure. A decrease of pore pressure $(P_f - P_o)$ results in increased effective stress in the depressurized region. Effective stresses increase because the overburden $S_v$ remains constant above the reservoir but the pore pressure decreases. The result is compaction of the reservoir (Fig. 8.1). Such deformation also affects neighboring formations and faults. Changes in ground surface elevation are refered as “subsidence". Differential displacements (for example across a fault) can result in casing damage and shearing. Significant compaction in the reservoir layer can result in casing buckling. The reduction of pore pressure also causes a reduction of total horizontal stress within the reservoir.

Figure 8.1: Schematic of deformation induced by reservoir depletion.

8.1.1 Rock compressibility and permeability

Reservoir depletion in horizontal, laterally extensive and thin reservoirs approximates to a one-dimensional-strain stress path, i.e. there is change in strain only in the vertical direction (Fig. 8.1). Such stress path results in increased effective stresses in both vertical and horizontal directions.

Increased effective stresses result in reduction of porosity and permeability in most cases. The permeability of fractured rocks tends to be more sensitive to stress than typical rock matrices. The reason is that permeability is proportional to the $d_{pore}^2$ in rock matrix, while permeability is proportional to the $w_{f}^3$ in fractures (Fig. 8.2). The variability of rock permeability with stress is called “fracture compressibility". The decline curves of unconventional formations are highly influenced by fracture compressibility.

Figure 8.2: Impact of increased effective stress on porosity and permeability

8.1.2 Linear poroelasticity solution

Let us use the theory of poroelasticity (Section 3.7.1) to solve for the changes of total and effective stresses with depletion. According to this theory, effective stress must be corrected for the Biot coefficient $\alpha$ so that,

$$\uuline{\sigma} = \uuline{S} - \alpha P_p \uuline{I}$$ (8.1)

We use this equation of effective stress together with linear isotropic elasticity in order to relate stresses to strain ( $\uuline{\sigma} = \uuline{C} \: \uuline{\varepsilon}$, and the assumption of one-dimensional strain $\uuline{\varepsilon} = [0,0,\varepsilon_{33},0,0,0]^T$ (3-vertical direction):

$$%compliance matrix \left[ \begin{array}{c} S_{11} - \alpha P... ... \cfrac{}{} \\ 0 \cfrac{}{}\\ 0 \cfrac{}{} \end{array}\right]$$ (8.2)

The equation corresponding to the 3rd row results in:

$$\varepsilon_{33} = \frac{S_{33} - \alpha P_p}{ \frac{E(1-\nu)}{(1+\nu)(1-2\nu)} }$$ (8.3)

The denominator is the constrained modulus $M = E(1-\nu)/(1+\nu)/(1-2\nu)$. Hence, the vertical strain in the reservoir layer is:

$$\Delta \varepsilon_{33} = -\frac{\alpha}{M} \Delta P_p$$ (8.4)

Remember that $S_{33}$ is the overburden stress and does not change with time or with reservoir pore pressure. Notice that depletion ( $\Delta P_p<0$) results in compaction ( $\Delta \varepsilon_{33}>0$). This deformation is linked to the reservoir compressibility. Hence, according to linear poroelasticity the uniaxial bulk compressibility is $C_{bp} = \alpha / M$ (See Section 3.3.5).

Combining Equations from rows 1 and 3 (or 2 and 3), results in

$$\Delta S_{11} = \alpha \frac{1-2\nu}{1-\nu} \: \Delta P_p$$ (8.5)

Depletion ( $\Delta P_p<0$) results in decreases of horizontal stress ( $\Delta S_{11}<0$). The same change of stress occurs in direction 2. The coefficient of proportionality in the previous equation is usually referred as $A = \alpha \frac{1-2\nu}{1-\nu}$ and varies typically from 0.5 to 0.9. The prediction of $S_{11}$ can be validated through hydraulic fracture tests that measure minimum horizontal total stress $S_{hmin}$ in places with normal faulting and strike slip regime.

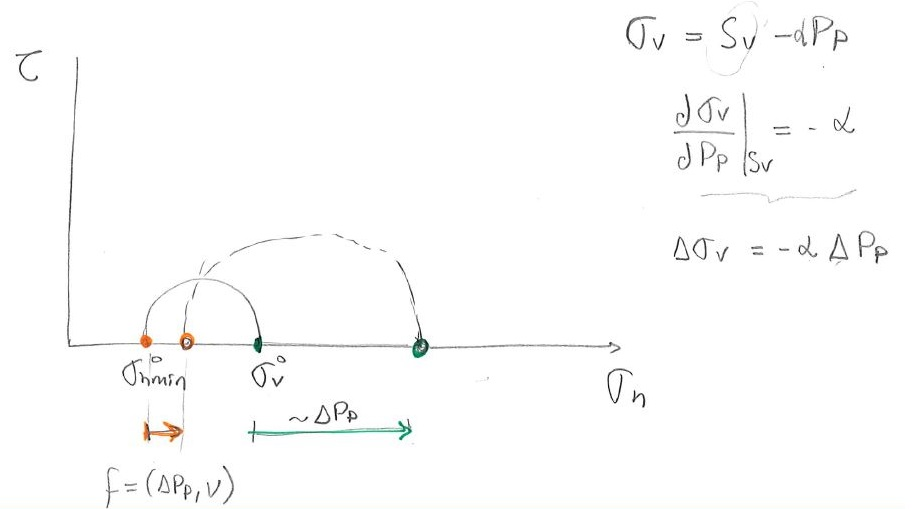
A total stress path plot describes the value of total stresses as a function of pore pressure (Fig. 8.3).

Figure 8.3: Total stress path plot. (a) Conceptual plot. (b) Example from the North Sea. The points corresponds to measurements from hydraulic fracture tests.

Depletion results in increased effective stresses. The change of vertical effective stress $\sigma_{33} = S_{33} - \alpha P_p$ (with $S_{33}$ constant) is

$$\Delta \sigma_{33} = - \alpha \Delta P_p$$ (8.6)

From Equation 8.5, the change of horizontal effective stress with pressure is

$$\Delta \sigma_{11} = - \alpha \frac{\nu}{1-\nu} \Delta P_p$$ (8.7)

Both, horizontal and vertical effective stresses increase with depth. This results in a shift of the Mohr circle to the right and up, i.e. increased mean effective stress and increased deviatoric stress (Fig. 8.4). Large compressive and shear stresses can result in rock failure under compression and shear. Grain crushing can significantly decrease the rock permeability.

Figure 8.4: Change of effective stress with depletion. Both horizontal and vertical effective stresses increase within the depleted reservoir.

PROBLEM 8.1: Calculate the following due to depletion of 35 MPa.

1. Displacement $\Delta H$ at the top of the reservoir.
2. Pore compressibility $C_{pp}$.
3. Change of total horizontal stress $\Delta S_{h}$.
4. Changes of effective vertical $\Delta \sigma_{v}$ and horizontal stresses $\Delta \sigma_{h}$.
5. Change of permeability $k/k_o$ with the following law ( $c_f = 0.25$ MPa$^{-1}$ ):

   $$k = k_o \: \exp \left[ -c_f (\sigma_h - \sigma_h^o) \right]$$

SOLUTION

1. The constrained modulus is

   $$M = \frac{E(1-\nu)}{(1+\nu)(1-2\nu)} = 14.8$$

   Then, the displacement at the top of the reservoir is $\Delta H = \Delta \varepsilon_{33} H$, where

   $$\varepsilon_{33} = -\frac{\alpha}{M} \Delta P_p = 0.21 \%$$

   Hence, $\Delta H = 0.21\% \: 100$   m $= 0.21$ m.

2. The bulk compressibility is

   $$C_{bp} = \frac{\alpha}{M} = 0.06 \times 10^{-9} \frac{1}{\text{Pa }} = 0.42 \times 10^{-6} \frac{1}{\text{psi }}$$

   Thus, the pore compressibility is

   $$C_{pp} = \frac{C_{bp}}{\phi} = 2.0 \times 10^{-6} \frac{1}{\text{psi }} = 2.0 \: \mu \text{sip}$$

3. The change of total horizontal stress is

   $$\Delta S_{h} = \alpha \frac{1-2\nu}{1-\nu} \: \Delta P_p = 0.716 \times (-35 ) \sim -25$$

4. The changes of effective stresses are

   $$\Delta \sigma_{33} = - \alpha \Delta P_p = - 0.9 \times (-35 ) = + 31.5$$

   $$\Delta \sigma_{11} = - \alpha \frac{\nu}{1-\nu} \Delta P_p = + 6.45$$

5. Last, the ratio between final and initial permeability $k/k_o$ is

   $$\frac{k}{k_o} = \exp \left[ -c_f (\sigma_h - \sigma_h^o) \right] ... ... -0.25 \text{ MPa}^{-1} (+6.45 \text{ MPa}) \right] \sim 0.2 \: \: \blacksquare$$