6.2 Kirsch solution for stresses around a cylindrical cavity

6.2.1 Cylindrical coordinate system

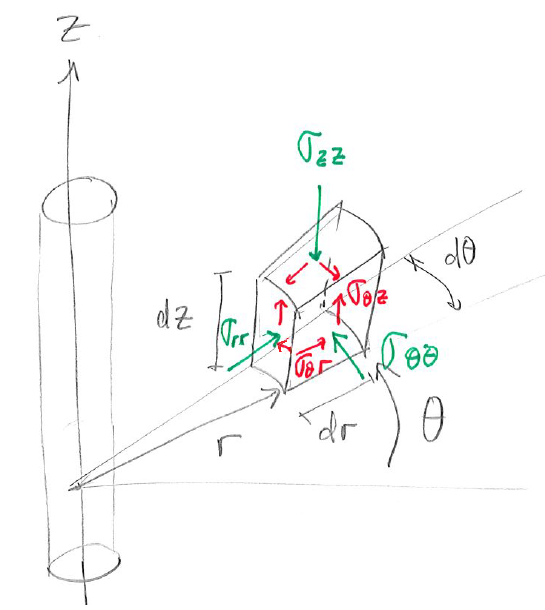
The cylindrical symmetry of a wellbore prompts the utilization of a cylindrical coordinate system rather than a rectangular cartesian coordinate system. The volume element of stresses in cylindrical coordinates is shown in Fig. 6.4. The distance $r$ is measured from the center axis of the wellbore. The angle $\theta$ is measured with respect to a predefined plane.

Figure 6.4: Infinitesimal volume element in cylindrical coordinates and associated normal and shear stresses.

The normal stresses are radial stress $\sigma _{rr}$, tangential or hoop stress $\sigma _{\theta \theta }$, and axial stress $\sigma_{zz}$. The shear stresses are $\sigma _{r\theta }$, $\sigma_{r z}$, and $\sigma_{\theta z}$.

6.2.2 Kirsch solution components

The Kirsch solution allows us to calculate normal and shear stresses around a circular cavity in a homogeneous linear elastic solid . The complete Kirsch solution assumes independent action of multiple factors, namely far-field isotropic stress, deviatoric stress, wellbore pressure and pore pressure.

1. Isotropic far-field stress: The solution for a compressive isotropic far field stress $\sigma _{\infty }$ is shown in Fig. 6.5. The presence of the wellbore amplifies compressive stresses 2 times $\sigma_{\theta \theta}/\sigma_{\infty}=2$ all around the wellbore wall in circumferential direction. The presence of the wellbore cavity also creates infinitely large stress anisotropy at the wellbore wall $\sigma_{\theta \theta}/\sigma_{rr}= \infty$ all around the wellbore wall, since $\sigma_{rr}=0$ in this case. Stresses decrease inversely proportional to $r^2$ and are neglible at $\sim$4 radii from the wellbore wall.

   Figure 6.5: Kirsch solution for far field isotropic stress $\sigma _{\infty }$.

   

2. Inner wellbore pressure: The solution for fluid wall pressure in the wellbore $P_W$ is shown in Fig. 6.6. We assume a non-porous solid now. This assumption will be relaxed later on. Wellbore pressure adds compression on the wellbore wall $\sigma_{rr} = +P_W$, and induces cavity expansion and tensile hoop stresses $\sigma_{\theta\theta} = - P_W$ all around the wellbore.

   Figure 6.6: Kirsch solution for wellbore pressure $P_W$.

   

3. Deviatoric stress: The solution for a deviatoric stress $\Delta \sigma$ aligned with $\theta = 0$ is shown in Fig. 6.7. The deviatoric stress results in compression on the wellbore wall $\sigma_{\theta \theta} = 3 \Delta \sigma$ at $\theta = \pi/2$ and $3\pi/2$, and in tension $\sigma_{\theta \theta} = - \Delta \sigma$ at $\theta = 0$ and $\pi$. Hence, the presence of the wellbore amplifies compressive stresses 3 times $\sigma_{\theta \theta}/\sigma_{\infty}=3$ at $\theta = \pi/2$ and $3\pi/2$. The variation of stresses around the wellbore depend on harmonic functions $\sin (\theta)$ and $\cos (\theta)$.

   Figure 6.7: Kirsch solution for far-field deviatoric stress $\Delta \sigma$.

   

4. Pore pressure: The last step consists in assuming a perfect mud-cake, so that, the effective stress wall support (as shown in Fig. 6.6) is $(P_W - P_p)$ instead of $P_W$.

6.2.3 Complete Kirsch solution

Consider a vertical wellbore subjected to horizontal stresses $S_{Hmax}$ and $S_{hmin}$, both principal stresses, vertical stress $S_v$, pore pressure $P_p$, and wellbore pressure $P_W$. The corresponding effective in-situ stresses are $\sigma_{Hmax}$, $\sigma_{hmin}$, and $\sigma _v$. The Kirsch solution for a wellbore with radius $a$ within a linear elastic and isotropic solid is:

$$\left\lbrace \begin{array}{rcl} \sigma_{rr} & = & (P_W - P_p)... ...left( \frac{a^2}{r^2} \right) \cos (2\theta) \end{array}\right.$$ (6.2)

where $\sigma _{rr}$ is the radial effective stress, $\sigma _{\theta \theta }$ is the tangential (hoop) effective stress, $\sigma _{r\theta }$ is the shear stress in a plane perpendicular to $r$ in tangential direction $\theta$, and $\sigma_{zz}$ is the vertical effective stress in direction $z$. The angle $\theta$ is the angle between the direction of $S_{Hmax}$ and the point at which stress is considered. The distance $r$ is measured from the center of the wellbore. For example, at the wellbore wall $r=a$.

An example of the solution of Kirsch equations for $S_{Hmax}=22$ MPa, $S_{hmin}=13$ MPa, and $P_W=P_p=10$ MPa is available in Figure 6.8. The plots show radial $\sigma _{rr}$ and tangential $\sigma _{\theta \theta }$ effective stresses, as well as the calculated principal stresses $\sigma _3$ and $\sigma_{1}$.

Figure 6.8: Example of solution of Kirsch equations. The effective radial stress at the wellbore wall is $P_W-P_p = 0$. Top: solution for radial $\sigma _{rr}$ and hoop $\sigma _{\theta \theta }$ stresses. Bottom: solution for principal stresses (eigenvalues from $\sigma _{\theta \theta }$, $\sigma _{rr}$, and $\sigma _{r\theta }$ ). Notice that $\sigma _1$ is the highest at top and bottom and $\sigma _3$ is the lowest at the sides. The influence of the cavity extend to a few wellbore radii.

Let us obtain $\sigma _{rr}$ and $\sigma _{\theta \theta }$ at the wellbore wall $r=a$. The radial stress for all $\theta$ is

$$\sigma_{rr}(r=a) = P_W - P_p$$ (6.3)

The hoop stress depends on $\theta$,

$$\sigma_{\theta \theta} (r=a) = -(P_W - P_p) +(\sigma_{Hmax}+\sigma_{hmin}) -2(\sigma_{Hmax}-\sigma_{hmin}) \cos (2\theta)$$ (6.4)

and it is the minimum at $\theta = 0$ and $\pi$ (azimuth of $S_{Hmax}$) and the maximum at $\theta = \pi/2$ and $3\pi/2$ (azimuth of $S_{hmin}$):

$$\left\lbrace \begin{array}{rcl} \sigma_{\theta \theta} (r=a,\... ..._W - P_p) +3 \: \sigma_{Hmax} -\sigma_{hmin} \end{array}\right.$$ (6.5)

These locations will be prone to develop tensile fractures ( $\theta = 0$ and $\pi$) and shear fractures ( $\theta = \pi/2$ and $3\pi/2$). The shear stress around the wellbore wall is $\sigma_{r \theta} = 0$. This makes sense because fluids (drilling mud) cannot apply steady shear stresses on the surface of a solid. Finally, the effective vertical stress is

$$\sigma_{zz} (r=a) = \sigma_v - 2\nu (\sigma_{Hmax}-\sigma_{hmin}) \cos (2\theta)$$ (6.6)