Next: 5.5 Critical state soil Up: 5. Inelasticity Previous: 5.3 Plastic strains Contents
The following data set has experimental data of shear strength for the Darley Dale Sandstone measured in an axisymmetric triaxial cell.
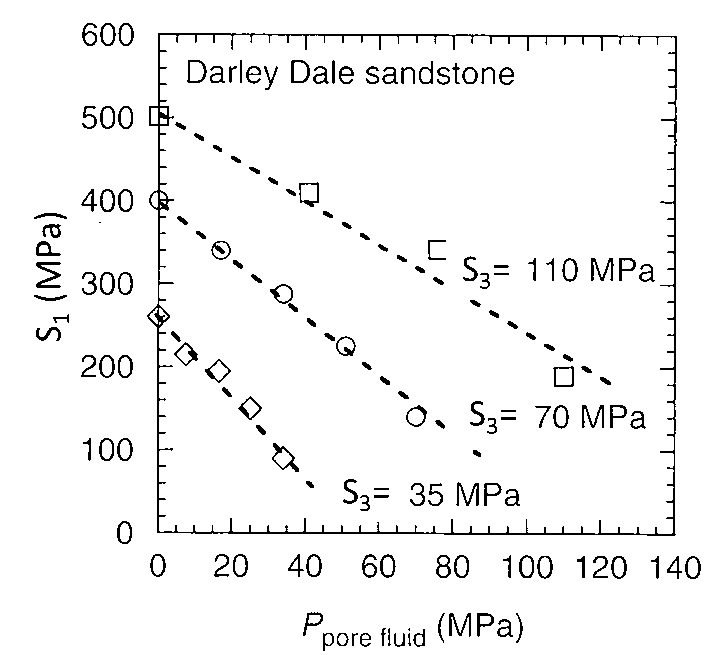 |
where 


 .
.
 and friction angle
and friction angle  from point (1) and draw the shear failure line together with Mohr circles at failure.
from point (1) and draw the shear failure line together with Mohr circles at failure.
 v.s.
v.s.
 space.
space.
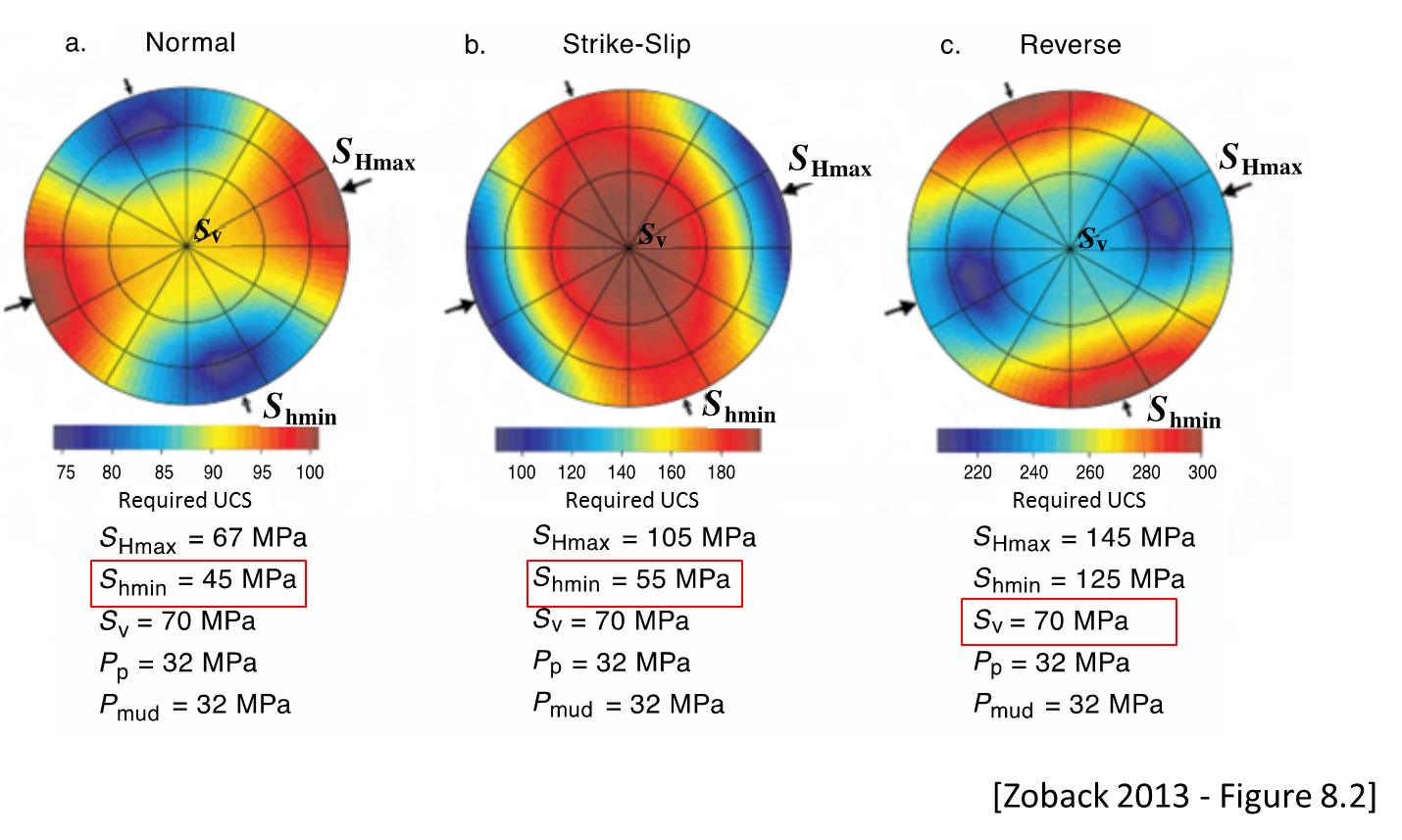
For this assignment you have to be able to calculate principal stresses on the wall of a wellbore at an arbitrary deviation and azimuth (See Chapter 6 of my notes “Wellbore stability” (https://dnicolasespinoza.github.io/) and Zoback's book Ch. 8).
Develop a script to compute and illustrate graphically (lower hemisphere projection):
 and a simple tensile strength criterion (independent of intermediate and maximum principal stresses), i.e., required
and a simple tensile strength criterion (independent of intermediate and maximum principal stresses), i.e., required  .
.
 and a simple unconfined compression strength criterion, i.e., required
and a simple unconfined compression strength criterion, i.e., required  .
.
 considering a Mohr-Coulomb shear failure criterion and the properties of the Darley Dale Sandstone from Exercise 1.
considering a Mohr-Coulomb shear failure criterion and the properties of the Darley Dale Sandstone from Exercise 1.
 considering a linear
considering a linear  v.s.
v.s.
 shear failure criterion and the properties of the Darley Dale Sandstone from Exercise 1.
shear failure criterion and the properties of the Darley Dale Sandstone from Exercise 1.
 considering a Modified Lade shear failure criterion (Zoback's book, p. 100) and the properties of the Darley Dale Sandstone from point 1.
considering a Modified Lade shear failure criterion (Zoback's book, p. 100) and the properties of the Darley Dale Sandstone from point 1.
Limit your wellbore breakout angle plots to





 |