Ideal orientation of faults

The ideal orientation of a hydraulic fracture is a plane perpendicular to the minimum principal stress $S_3$ direction. Similarly, we can also tell what would be the orientation of ideal conjugate pairs of shear fractures (faults) for a given state of stress. The dip and strike will depend on $S_1$, $S_3$, and the friction angle $\varphi$ (Fig. 5.17). Such ideal conjugate pair of shear fractures would be located:

• in planes that are in between the planes perpendicular to $S_1$ and $S_3$,
• in planes that are co-linear with $S_2$,
• in planes that are at 45 $^{\circ} + \varphi/2$ from the plane perpendicular to $S_1$

Notice that all these angles vary according to the stress regime. Faults formed in NF stress regime tend to be steep. Faults formed in RF stress regime are not too steep. Faults formed in SS stress regime are vertical.

Figure 5.17: Summary of ideal (a) hydraulic fracture orientation, (b) normal fault orientation, (c) strike-slip fault orientation, and (d) thrust (reverse) faults orientation.

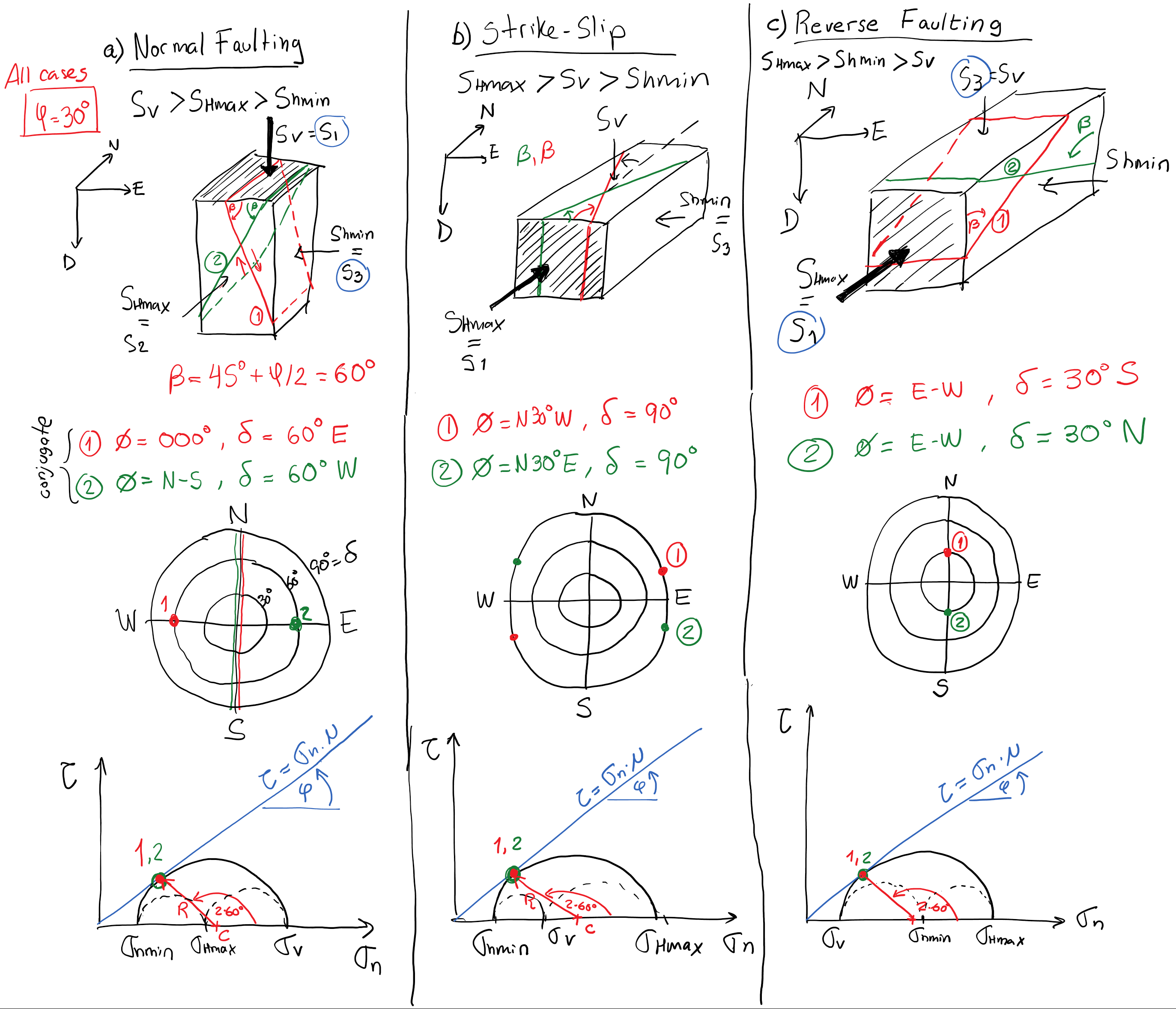PROBLEM 5.1: Find the ideal orientation of a hydraulic fracture and faults (shear fractures) at a location subjected to the following state of stress and conditions:

• Stress regime: Normal faulting
• $S_v$ is a principal stress
• Azimuth of $S_{hmin}$ is N60$^{\circ }$W
• Friction angle $\varphi$ = 30$^{\circ }$.

SOLUTION
First, recognize the planes of $S_1$ and $S_3$ and their orientations with respect to the geographical coordinate system. The plane of $S_1$ in this case is a horizontal plane ($S_v$ plane, a principal stress) and the plane of $S_3$ is a vertical plane perpendicular to $S_{hmin}$.

A hydraulic fracture would be perpendicular to $S_3$, in this case $S_{hmin}$. Hence, the strike is $\phi_{HF} = 030^{\circ}$ and the dip is $\delta_{HF} = 90^{\circ}$ because $S_3$ is horizontal.

Faults will also depend on the friction angle. In this case, the failure angle is:

$$\beta = 45^{\circ} + \varphi / 2 = 45^{\circ} + 30^{\circ} / 2 = 60^{\circ}$$

The fault planes are at $\beta$ going from the plane of $S_1$ to the plane of $S_3$. Thus, the strike of the two possible faults is $\phi_{F1} = \phi_{F2} = 030^{\circ}$ and the dips are $\delta_{F1} = 60^{\circ}$SE and $\delta_{F1} = 60^{\circ}$NW. $\: \: \blacksquare$

PROBLEM 5.2: Find the ideal orientation of a hydraulic fracture and faults (shear fractures) at a location subjected to the following state of stress and conditions:

• Stress regime: Strike-slip faulting
• $S_v$ is a principal stress
• Azimuth of $S_{Hmax}$ is 010$^{\circ }$
• Friction angle $\varphi$ = 40$^{\circ }$.

SOLUTION
First, recognize the planes of $S_1$ and $S_3$ and their orientations with respect to the geographical coordinate system. The plane of $S_1$ in this case is a vertical plane ($S_{Hmax}$ plane) and the plane of $S_3$ is another vertical plane perpendicular to $S_{hmin}$.

A hydraulic fracture would be perpendicular to $S_3$, in this case $S_{hmin}$. Hence, the strike is $\phi_{HF} = 010^{\circ}$ and the dip is $\delta_{HF} = 90^{\circ}$ because $S_3$ is horizontal.

Faults will also depend on the friction angle. In this case, the failure angle is:

$$\beta = 45^{\circ} + \varphi / 2 = 45^{\circ} + 40^{\circ} / 2 = 65^{\circ}$$

The fault planes are at $\beta$ going from the plane of $S_1$ to the plane of $S_3$. Thus, the strikes of the two possible faults are $\phi_{F1} = 345^{\circ}$ and $\phi_{F2} = 035^{\circ}$, the dip is $\delta_{F1} = \delta_{F2} = 90^{\circ}$. $\: \: \blacksquare$